题目内容
定义在R上的函数f(x)满足f(x)=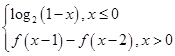 ,则f(2 013)=________.
,则f(2 013)=________.
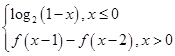 ,则f(2 013)=________.
,则f(2 013)=________.0
当x>0时,∵f(x)=f(x-1)-f(x-2),
∴f(x+1)=f(x)-f(x-1),
∴f(x+1)=-f(x-2),即f(x+3)=-f(x),
∴f(x+6)=f(x),即当x>0时,
函数f(x)的周期是6.
又∵f(2 013)=f(335×6+3)=f(3),
由已知得f(-1)=log22=1,f(0)=0,
f(1)=f(0)-f(-1)=0-1=-1,
f(2)=f(1)-f(0)=-1-0=-1,
f(3)=f(2)-f(1)=-1-(-1)=0,
∴f(2 013)=0.
∴f(x+1)=f(x)-f(x-1),
∴f(x+1)=-f(x-2),即f(x+3)=-f(x),
∴f(x+6)=f(x),即当x>0时,
函数f(x)的周期是6.
又∵f(2 013)=f(335×6+3)=f(3),
由已知得f(-1)=log22=1,f(0)=0,
f(1)=f(0)-f(-1)=0-1=-1,
f(2)=f(1)-f(0)=-1-0=-1,
f(3)=f(2)-f(1)=-1-(-1)=0,
∴f(2 013)=0.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
 的定义域为________.
的定义域为________.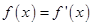 的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=2x,h(x)=
的实数根x0叫做函数f(x)的“新驻点”,若函数g(x)=2x,h(x)=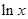 ,φ(x)=x3(x≠0)的“新驻点”分别为A,b,c,则A,b,c的大小关系为( )
,φ(x)=x3(x≠0)的“新驻点”分别为A,b,c,则A,b,c的大小关系为( )



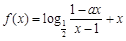 为奇函数,
为奇函数,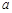 为常数.
为常数.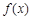 在
在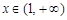 上的单调性,并说明理由;
上的单调性,并说明理由;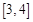 上的每一个
上的每一个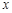 值,不等式
值,不等式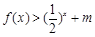 恒成立,求实数
恒成立,求实数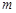 的取值范围.
的取值范围.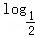 x 的零点个数为( )
x 的零点个数为( )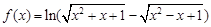 的值域为 .
的值域为 . 的定义域是 .
的定义域是 . .
.