题目内容
设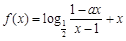 为奇函数,
为奇函数,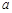 为常数.
为常数.
(1)求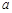 的值;
的值;
(2)判断函数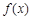 在
在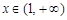 上的单调性,并说明理由;
上的单调性,并说明理由;
(3)若对于区间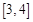 上的每一个
上的每一个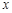 值,不等式
值,不等式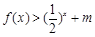 恒成立,求实数
恒成立,求实数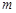 的取值范围.
的取值范围.
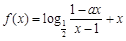 为奇函数,
为奇函数,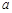 为常数.
为常数.(1)求
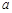 的值;
的值;(2)判断函数
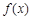 在
在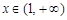 上的单调性,并说明理由;
上的单调性,并说明理由;(3)若对于区间
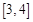 上的每一个
上的每一个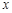 值,不等式
值,不等式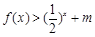 恒成立,求实数
恒成立,求实数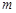 的取值范围.
的取值范围.(1)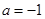
(2)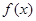 在
在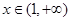 上是增函数
上是增函数
(3)
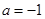
(2)
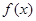 在
在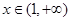 上是增函数
上是增函数(3)

解:(1)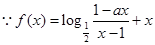 为奇函数,
为奇函数,
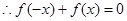 对定义域内的任意
对定义域内的任意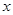 都成立,
都成立,
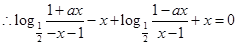 ,
,
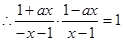 , 解,得
, 解,得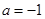 或
或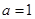 (舍去).
(舍去).
(2)由(1)知: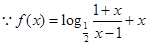 ,
,
任取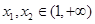 ,设
,设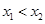 ,则:
,则:
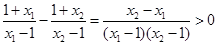 ,
,
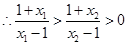 ,
,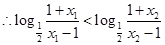
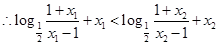 ,
,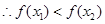
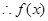 在
在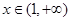 上是增函数.
上是增函数.
(3)令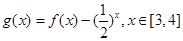 ,
,
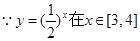 上是减函数,
上是减函数,
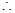 由(2)知,
由(2)知,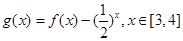 是增函数,
是增函数,
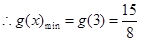 ,
,
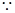 对于区间
对于区间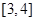 上的每一个
上的每一个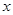 值,不等式
值,不等式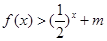 恒成立,
恒成立,
即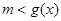 恒成立,
恒成立, 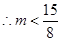 .
.
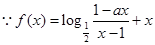 为奇函数,
为奇函数,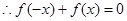 对定义域内的任意
对定义域内的任意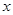 都成立,
都成立, 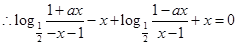 ,
,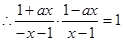 , 解,得
, 解,得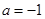 或
或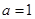 (舍去).
(舍去).(2)由(1)知:
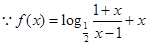 ,
,任取
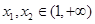 ,设
,设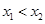 ,则:
,则: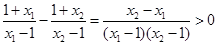 ,
,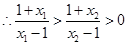 ,
,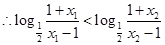
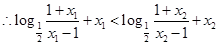 ,
,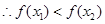
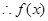 在
在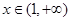 上是增函数.
上是增函数.(3)令
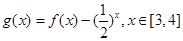 ,
, 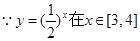 上是减函数,
上是减函数,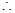 由(2)知,
由(2)知,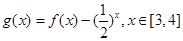 是增函数,
是增函数,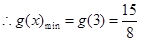 ,
,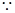 对于区间
对于区间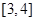 上的每一个
上的每一个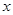 值,不等式
值,不等式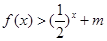 恒成立,
恒成立,即
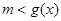 恒成立,
恒成立, 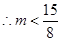 .
.
练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
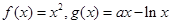 ,
,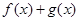 在
在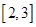 上是减函数,求实数
上是减函数,求实数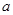 的取值范围;
的取值范围;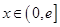 (
(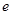 是自然常数)时,函数
是自然常数)时,函数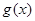 的最小值是3,若存在,求出
的最小值是3,若存在,求出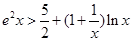 .
.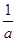 +
+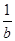 =2,则m=________.
=2,则m=________.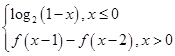 ,则f(2 013)=________.
,则f(2 013)=________. )
) ,b+1)
,b+1) 对任意的
对任意的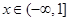 恒成立,则
恒成立,则 的取值范围是( )
的取值范围是( )



 ,且
,且 ,则
,则 ( )
( )