题目内容
椭圆与双曲线有许多优美的对偶性质,对于椭圆有如下命题:已知A、F、B分别是优美椭圆 +
+ =1(a>b>0)(离心率为黄金分割比
=1(a>b>0)(离心率为黄金分割比 的椭圆)的左顶点、右焦点和上顶点,则AB⊥BF.那么对于双曲线则有如下命题:已知A、F、B分别是优美双曲线
的椭圆)的左顶点、右焦点和上顶点,则AB⊥BF.那么对于双曲线则有如下命题:已知A、F、B分别是优美双曲线 -
- =1(a>b>0)(离心率为黄金分割比的倒数
=1(a>b>0)(离心率为黄金分割比的倒数 的双曲线)的左顶点、右焦点和其虚轴的上端点,则有
的双曲线)的左顶点、右焦点和其虚轴的上端点,则有
- A.AB⊥BF
- B.AF⊥BF
- C.AB⊥AF
- D.AB∥BF
A
分析:根据图象可知AB2=a2+b2=c2,BF2=b2+c2=2c2-a2,进而根据 =
= 求得AF2=
求得AF2=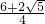 c2,进而表示出AB2+BF2,最后可得AF2=AB2+BF2,根据勾股定理判断出AB⊥BF.
c2,进而表示出AB2+BF2,最后可得AF2=AB2+BF2,根据勾股定理判断出AB⊥BF.
解答: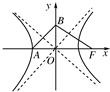 解:如图,AB2=a2+b2=c2,BF2=b2+c2=2c2-a2,
解:如图,AB2=a2+b2=c2,BF2=b2+c2=2c2-a2,
∵ =
= ,
,
∴ =
=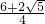 ,
,
∴AF2=( c+c)2=
c+c)2=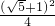 c2=
c2=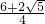 c2,
c2,
而AB2+BF2=c2+2c2-a2=3c2-( c)2=3c2-
c)2=3c2-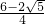 c2=
c2=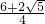 c2,
c2,
∴AF2=AB2+BF2,故AB⊥BF.
故选A
点评:本题主要考查了双曲线的简单性质.要利用好双曲线标准方程中的a,b和c的关系.
分析:根据图象可知AB2=a2+b2=c2,BF2=b2+c2=2c2-a2,进而根据
 =
= 求得AF2=
求得AF2=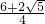 c2,进而表示出AB2+BF2,最后可得AF2=AB2+BF2,根据勾股定理判断出AB⊥BF.
c2,进而表示出AB2+BF2,最后可得AF2=AB2+BF2,根据勾股定理判断出AB⊥BF.解答:
 解:如图,AB2=a2+b2=c2,BF2=b2+c2=2c2-a2,
解:如图,AB2=a2+b2=c2,BF2=b2+c2=2c2-a2,∵
 =
= ,
,∴
 =
=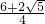 ,
,∴AF2=(
 c+c)2=
c+c)2=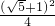 c2=
c2=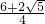 c2,
c2,而AB2+BF2=c2+2c2-a2=3c2-(
 c)2=3c2-
c)2=3c2-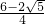 c2=
c2=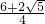 c2,
c2,∴AF2=AB2+BF2,故AB⊥BF.
故选A
点评:本题主要考查了双曲线的简单性质.要利用好双曲线标准方程中的a,b和c的关系.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
 +
+ =1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=-
=1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=- .那么对于双曲线则有如下命题:AB是双曲线
.那么对于双曲线则有如下命题:AB是双曲线 -
- =1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .
=1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .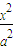 +
+ =1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=-
=1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB=- .那么对于双曲线则有如下命题:AB是双曲线
.那么对于双曲线则有如下命题:AB是双曲线 -
- =1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= .
=1(a>0,b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM•kAB= . +
+ =1(a>b>0)(离心率为黄金分割比
=1(a>b>0)(离心率为黄金分割比 的椭圆)的左顶点、右焦点和上顶点,则AB⊥BF.那么对于双曲线则有如下命题:已知A、F、B分别是优美双曲线
的椭圆)的左顶点、右焦点和上顶点,则AB⊥BF.那么对于双曲线则有如下命题:已知A、F、B分别是优美双曲线 -
- =1(a>b>0)(离心率为黄金分割比的倒数
=1(a>b>0)(离心率为黄金分割比的倒数 的双曲线)的左顶点、右焦点和其虚轴的上端点,则有( )
的双曲线)的左顶点、右焦点和其虚轴的上端点,则有( )