题目内容
已知函数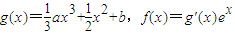 ,其中e为自然对数的底数
,其中e为自然对数的底数(I)若函数g(x)在点(1,g(1))处的切线与直线2x-y+1=0垂直,求实数a的值;
(II)若f(x)在[-1,1]上是单调增函数,求实数a的取值范围;
(III)当a=0时,求整数k的所有值,使方程f(x)=x+2在[k,k+1]上有解.
【答案】分析:(I)根据求导公式和法则求出函数的导数,再求出切线的斜率,由导数的几何意义列出方程求出a的值;
(II)求出导函数后,将条件转化为“f′(x)=[ax2+(2a+1)x+1]ex≥0在[-1,1]上恒成立”,再进一步转化后构造g(x)=ax2+(2a+1)x+1,再分类讨论:a=0时和a≠0时,分别根据△=(2a+1)2-4a=4a2+1>0和特值g(0)=1>0,列出等价条件求出a的取值范围;
(III)根据条件将原方程等价于“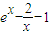 =0”,再构造函数h(x)=
=0”,再构造函数h(x)=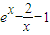 ,求导函数再确定h(x)在(-∞,0)和(0,+∞)内的单调性,再由特殊的函数值确定方程f(x)=x+2有且只有两个实数根的区间,故可得k的值.
,求导函数再确定h(x)在(-∞,0)和(0,+∞)内的单调性,再由特殊的函数值确定方程f(x)=x+2有且只有两个实数根的区间,故可得k的值.
解答:解:(I)由题意得,g′(x)=ax2+x,
∵在点(1,g(1))处的切线与直线2x-y+1=0垂直,
∴在点(1,g(1))处的切线斜率为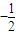 ,即g′(1)=a+1=
,即g′(1)=a+1=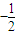 ,
,
解得a=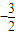 ,
,
(II)由(I)得,f(x)=g′(x)ex=(ax2+x)ex,
则f′(x)=(2ax+1)ex+(ax2+x)ex=[ax2+(2a+1)x+1]ex,
∵f(x)在[-1,1]上是单调增函数,
∴f′(x)=[ax2+(2a+1)x+1]ex≥0在[-1,1]上恒成立,
即ax2+(2a+1)x+1≥0在[-1,1]上恒成立,
①当a=0时,f′(x)=(x+1)ex,f′(x)≥0在[-1,1]上恒成立,
当且仅当x=-1时取等号,故a=0符合要求;(6分)
②当a≠0时,令g(x)=ax2+(2a+1)x+1,
因为△=(2a+1)2-4a=4a2+1>0,所以g(x)=0有两个不相等的实数根x1,x2,不妨设x1>x2,
因此f(x)有极大值又有极小值.
若a>0,因为g(-1)•g(0)=-a<0,所以f(x)在(-1,1)内有极值点,故f(x)在[-1,1]上不单调.
若a<0,可知x1>0>x2,因为g(x)的图象开口向下,要使f(x)在[-1,1]上单调,
因为g(0)=1>0,必须满足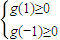 ,即
,即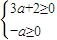 ,得
,得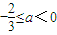 ,
,
综上可知,a的取值范围是[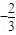 ,0],
,0],
(III)当a=0时,方程即为xex=x+2,由于ex>0,所以x=0不是方程的解,
所以原方程等价于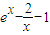 =0,令h(x)=
=0,令h(x)=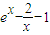 ,
,
因为h′(x)=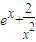 >0对于x∈(-∞,0)∪(0,+∞)恒成立,
>0对于x∈(-∞,0)∪(0,+∞)恒成立,
所以h(x)在(-∞,0)和(0,+∞)内是单调增函数,(13分)
又h(1)=e-3<0,h(2)=e2-2>0,h(-3)=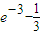 <0,h(-2)=e-2>0,
<0,h(-2)=e-2>0,
所以方程f(x)=x+2有且只有两个实数根,且分别在区间[1,2]和[-3,-2]上,
所以整数k的所有值为{-3,1}.
点评:本题考查了导数的几何意义,导数与函数的单调性关系,以及证明不等式转化为恒成立问题等,考查了分类讨论思想、转化思想和构造函数方法.
(II)求出导函数后,将条件转化为“f′(x)=[ax2+(2a+1)x+1]ex≥0在[-1,1]上恒成立”,再进一步转化后构造g(x)=ax2+(2a+1)x+1,再分类讨论:a=0时和a≠0时,分别根据△=(2a+1)2-4a=4a2+1>0和特值g(0)=1>0,列出等价条件求出a的取值范围;
(III)根据条件将原方程等价于“
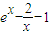 =0”,再构造函数h(x)=
=0”,再构造函数h(x)=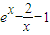 ,求导函数再确定h(x)在(-∞,0)和(0,+∞)内的单调性,再由特殊的函数值确定方程f(x)=x+2有且只有两个实数根的区间,故可得k的值.
,求导函数再确定h(x)在(-∞,0)和(0,+∞)内的单调性,再由特殊的函数值确定方程f(x)=x+2有且只有两个实数根的区间,故可得k的值.解答:解:(I)由题意得,g′(x)=ax2+x,
∵在点(1,g(1))处的切线与直线2x-y+1=0垂直,
∴在点(1,g(1))处的切线斜率为
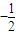 ,即g′(1)=a+1=
,即g′(1)=a+1=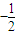 ,
,解得a=
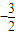 ,
,(II)由(I)得,f(x)=g′(x)ex=(ax2+x)ex,
则f′(x)=(2ax+1)ex+(ax2+x)ex=[ax2+(2a+1)x+1]ex,
∵f(x)在[-1,1]上是单调增函数,
∴f′(x)=[ax2+(2a+1)x+1]ex≥0在[-1,1]上恒成立,
即ax2+(2a+1)x+1≥0在[-1,1]上恒成立,
①当a=0时,f′(x)=(x+1)ex,f′(x)≥0在[-1,1]上恒成立,
当且仅当x=-1时取等号,故a=0符合要求;(6分)
②当a≠0时,令g(x)=ax2+(2a+1)x+1,
因为△=(2a+1)2-4a=4a2+1>0,所以g(x)=0有两个不相等的实数根x1,x2,不妨设x1>x2,
因此f(x)有极大值又有极小值.
若a>0,因为g(-1)•g(0)=-a<0,所以f(x)在(-1,1)内有极值点,故f(x)在[-1,1]上不单调.
若a<0,可知x1>0>x2,因为g(x)的图象开口向下,要使f(x)在[-1,1]上单调,
因为g(0)=1>0,必须满足
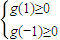 ,即
,即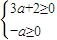 ,得
,得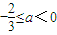 ,
,综上可知,a的取值范围是[
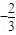 ,0],
,0],(III)当a=0时,方程即为xex=x+2,由于ex>0,所以x=0不是方程的解,
所以原方程等价于
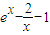 =0,令h(x)=
=0,令h(x)=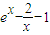 ,
,因为h′(x)=
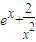 >0对于x∈(-∞,0)∪(0,+∞)恒成立,
>0对于x∈(-∞,0)∪(0,+∞)恒成立,所以h(x)在(-∞,0)和(0,+∞)内是单调增函数,(13分)
又h(1)=e-3<0,h(2)=e2-2>0,h(-3)=
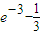 <0,h(-2)=e-2>0,
<0,h(-2)=e-2>0,所以方程f(x)=x+2有且只有两个实数根,且分别在区间[1,2]和[-3,-2]上,
所以整数k的所有值为{-3,1}.
点评:本题考查了导数的几何意义,导数与函数的单调性关系,以及证明不等式转化为恒成立问题等,考查了分类讨论思想、转化思想和构造函数方法.

练习册系列答案
相关题目
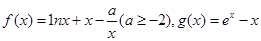 ,其中e为自然对数的底数,且当x>0时
,其中e为自然对数的底数,且当x>0时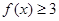 恒成立.
恒成立. 的单调区间;
的单调区间; .
. (其中e为自然对数)
(其中e为自然对数) 的极值。
的极值。 (常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。
(常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。 ,其中e为自然对数的底数.
,其中e为自然对数的底数.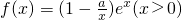 ,其中e为自然对数的底数.
,其中e为自然对数的底数. 在(1,l:x=1)处的切线与坐标轴围成的面积;
在(1,l:x=1)处的切线与坐标轴围成的面积; 存在一个极大值点和一个极小值点,且极大值与极小值的积为e5,求a的值.
存在一个极大值点和一个极小值点,且极大值与极小值的积为e5,求a的值.