题目内容
(本小题满分12分)已知函数 (其中e为自然对数)
(其中e为自然对数)
(1)求F(x)="h" (x) 的极值。
的极值。
(2)设 (常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。
(常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。
【答案】
(1)F(x)取极小值为0(2) 若
若
 1时,即0<a
1时,即0<a 2,G(x)在(1,
2,G(x)在(1, )递增.,无极值。若
)递增.,无极值。若 >1时,即a>2,G(x)在(1,
>1时,即a>2,G(x)在(1, )递减,在(
)递减,在( ,
, ))递增。所以
))递增。所以 处有极小值,极小值为
处有极小值,极小值为
【解析】
试题分析:(1)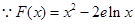 (x>0)
(x>0)

当0<x< 时,
时,  <0, 此时F(x)递减,
<0, 此时F(x)递减,
当x> 时,
时,  >0,此时F(x)递增
>0,此时F(x)递增
当x= 时,F(x)取极小值为0 ……6分
时,F(x)取极小值为0 ……6分
(2)可得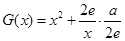 =
=
 , ……9分
, ……9分
当 x<
x< 时,G(x)递减,当x>
时,G(x)递减,当x> 时,G(x)递增 x>1,
时,G(x)递增 x>1,  若
若
 1时,即0<a
1时,即0<a 2,G(x)在(1,
2,G(x)在(1, )递增.,无极值。若
)递增.,无极值。若 >1时,即a>2,G(x)在(1,
>1时,即a>2,G(x)在(1, )递减,在(
)递减,在( ,
, ))递增。所以
))递增。所以 处有极小值,极小值为
处有极小值,极小值为 ……
12分
……
12分
考点:利用函数的导数求极值,单调区间
点评:本题第二问中求单调区间,极值时要注意对参数a的讨论,当a取不同值时,函数在x>1的范围内的单调性不同

练习册系列答案
相关题目