题目内容
已知函数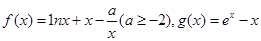 ,其中e为自然对数的底数,且当x>0时
,其中e为自然对数的底数,且当x>0时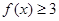 恒成立.
恒成立.
(Ⅰ)求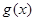 的单调区间;
的单调区间;
(Ⅱ)求实数a的所有可能取值的集合;
(Ⅲ)求证: .
.
【答案】
(Ⅰ) 减区间是 ,增区间是
,增区间是 ;(Ⅱ)
;(Ⅱ)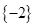 ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)确定定义域,求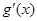 ,由
,由
 求得增区间,由
求得增区间,由 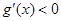 求得减区间;(Ⅱ)利用在区间
求得减区间;(Ⅱ)利用在区间 上,
上,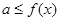 恒成立,则
恒成立,则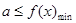 求解;(Ⅲ)利用构造法,构造新函数求解.
求解;(Ⅲ)利用构造法,构造新函数求解.
试题解析:(Ⅰ)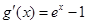 ,
,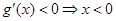 ,
,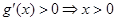 ,
,
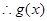 的减区间是
的减区间是 ,增区间是
,增区间是 . (2分)
. (2分)
(Ⅱ)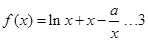 恒成立,即
恒成立,即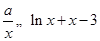 ,
,
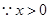 ,
,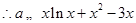 恒成立. (3分)
恒成立. (3分)
设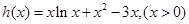 ,
,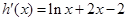 ,
,
由于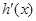 在
在 上是增函数,且
上是增函数,且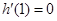 ,
,
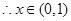 时,
时,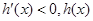 是减函数,
是减函数,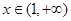 时,
时,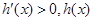 是增函数,
是增函数,
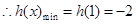 ,从而若
,从而若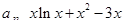 恒成立,必有
恒成立,必有 . (5分)
. (5分)
又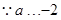 ,
,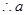 的取值集合为
的取值集合为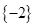 . (6分)
. (6分)
(Ⅲ)由(Ⅰ)知,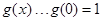 ,即
,即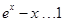 ,当且仅当
,当且仅当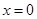 时等号成立,
时等号成立,
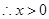 时,有
时,有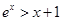 .
.
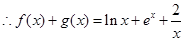
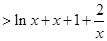 , (9分)
, (9分)
设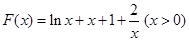 ,
,
则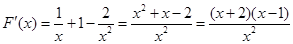 ,
,
当 时,
时,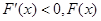 是减函数,
是减函数,
当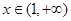 时,
时,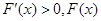 是增函数,
是增函数,
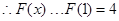 ,即
,即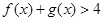 成立. (12分)
成立. (12分)
考点:导数法判断函数的单调性,恒成立,构造法.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
 (其中e为自然对数)
(其中e为自然对数) 的极值。
的极值。 (常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。
(常数a>0),当x>1时,求函数G(x)的单调区间,并在极值存在处求极值。 ,其中e为自然对数的底数.
,其中e为自然对数的底数.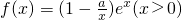 ,其中e为自然对数的底数.
,其中e为自然对数的底数. 在(1,l:x=1)处的切线与坐标轴围成的面积;
在(1,l:x=1)处的切线与坐标轴围成的面积; 存在一个极大值点和一个极小值点,且极大值与极小值的积为e5,求a的值.
存在一个极大值点和一个极小值点,且极大值与极小值的积为e5,求a的值.