题目内容
一束光线从点A(-3,9)出发经x轴反射到圆C:(x-2)2+(y-3)2=1的最短路程是 .
12
解析试题分析:由圆C的方程找出圆心C的坐标及圆的半径r,找出C关于x轴的对称点C′,连接AC′,利用两点间的距离公式求出|AC′|的长,用|AC′|的长减去圆的半径,即可得到光线的最短路程.作出圆心C关于x的对称点C′,连接AC′,由圆C:(x-2)2+(y-3)2=1,得到圆心C坐标为(2,3),圆的半径r=1,
可得C′的坐标为(2,-3),又A(-3,9),那么两点之间的距离为AC′=13,因此可知,最短的路程为13-1=12,故答案为12.
考点:对称的性质
点评:此题考查了对称的性质,两点间的距离公式,以及圆的标准方程,利用了数形结合的思想,解题的思路为根据题意画出图形,作出圆关于x轴的对称图形,利用两点之间线段最短可得出光线的最短距离

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 的图像与曲线
的图像与曲线 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数 的取值范围为 .
的取值范围为 .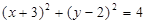 相切的直线方程是___________.
相切的直线方程是___________. ,若以坐标原点
,若以坐标原点 为极点,
为极点,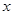 轴的正半轴为极轴,则该圆的极坐标方程可写为 .
轴的正半轴为极轴,则该圆的极坐标方程可写为 . ,AB=3,则切线AD的长为___ _____.
,AB=3,则切线AD的长为___ _____.
 经过点
经过点 和
和 ,且圆心
,且圆心 上,则圆
上,则圆 轴上,且过两点
轴上,且过两点 的圆的方程为 .
的圆的方程为 .  (
( 是实数)与圆
是实数)与圆 相交于
相交于 两点,且
两点,且 (
( 是坐标原点)是直角三角形,则点
是坐标原点)是直角三角形,则点 与点
与点 之间距离的最小值是 .
之间距离的最小值是 . 关于
关于 轴对称的圆的方程为______________.
轴对称的圆的方程为______________.