题目内容
【题目】设复数z=2m+(4-m2)i,其中i为虚数单位,当实数m取何值时,复数z对应的点:
(1)位于虚轴上;
(2)位于一、三象限;
(3)位于以原点为圆心,以4为半径的圆上.
【答案】(1)m=0;
(2)m∈(-∞,-2)∪(0,2);
(3)m=0或m=±2.
【解析】
(1)根据复数的几何意义求出点的坐标,利用点在虚轴上,建立方程关系即可;
(2)根据点在一三象限,建立不等式关系即可;
(3)根据点与圆的方程进行求解即可.
(1)复数z对应的点位于虚轴上,
则![]() .
.
∴m=0时,复数z对应的点位于虚轴上.
(2)复数z对应的点位于一、三象限,
则![]()
![]() m<-2或0<m<2.
m<-2或0<m<2.
∴当m∈(-∞,-2)∪(0,2)时,复数z对应的点位于一、三象限.
(3)复数z对应的点位于以原点为圆心,以4为半径的圆上,
则![]() m=0或m=±2.
m=0或m=±2.
∴m=0或m=±2时,复数z对应的点位于以原点为圆心,以4为半径的圆上.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
【题目】某地区城乡居民人民币储蓄存款(年底余额)如下表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
时间代号t | 1 | 2 | 3 | 4 | 5 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
(1)求y关于t的线性回归方程![]() ;
;
(2)用所求线性回归方程预测该地区2019年(t=6)的人民币储蓄存款.
(回归方程![]() 中,
中,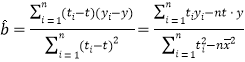 ,
,![]() )
)