题目内容
【题目】如图在平面直角坐标系xOy中,圆C的方程为![]() ,且圆C与y轴交于M,N两点(点N在点M的上方),直线
,且圆C与y轴交于M,N两点(点N在点M的上方),直线![]() 与圆C交于A,B两点。
与圆C交于A,B两点。
(1)若![]() ,求实数k的值。
,求实数k的值。
(2)设直线AM,直线BN的斜率分别为![]() ,若存在常数
,若存在常数![]() 使得
使得![]() 恒成立?若存在,求出a的值.若不存在请说明理由。
恒成立?若存在,求出a的值.若不存在请说明理由。
(3)若直线AM与直线BN相较于点P,求证点P在一条定直线上。

【答案】(1)![]() .
.
(2)存在实数![]() ,使得
,使得![]() 恒成立;理由见解析.
恒成立;理由见解析.
(3)证明见解析.
【解析】分析:(1)先设出直线的方程,利用圆中的特殊三角形:弦心距,半弦长和圆的半径构成直角三角形,勾股定理求得结果;
(2)先假设存在,利用题的条件,得到其相关的式子,求得对应的值,得到结果;
(3)根据题意,得到点所满足的条件,从而求得结果.
详解:(1)∵圆![]() :
:![]() ∴圆心
∴圆心![]() ,半径
,半径![]()
∵直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点,且
两点,且![]()
∴圆心到![]() 的距离为
的距离为![]() ∴
∴![]() ,解得:
,解得:![]()
∵![]() ∴
∴![]()
(2)∵圆![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 上方)
上方)
∴![]() ∴
∴![]() ,设
,设![]()
直线![]() 与圆
与圆![]() 方程联立:
方程联立:![]() ,化简得:
,化简得:![]()
∴![]() ,同理可求:
,同理可求:![]()
∵![]() 三点共线,且
三点共线,且![]() ,
,![]()
∴![]() ,化简得:
,化简得:![]()
∵![]() ∴
∴![]() ,即
,即![]()
∴存在实数![]() ,使得
,使得![]() 恒成立.
恒成立.
(3)设![]() ∴
∴![]() 且
且 ![]() ∴
∴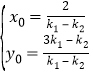
由(2)知:![]() ,代入得:
,代入得:![]() 为定值
为定值
∴点![]() 在定直线
在定直线![]() 上.
上.

练习册系列答案
相关题目


