题目内容
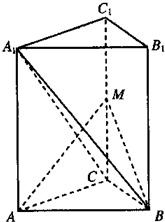 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,CA=
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CB=1,CA=| 3 |
| 6 |
(Ⅰ)求异面直线A1B与AC所成角的余弦值;
(Ⅱ)求证:AM⊥平面A1BC;
(Ⅲ)求二面角M-AB-C的正切值.
分析:(Ⅰ)说明∠BA1C1是异面直线A1B与AC所成的角,解三角形求异面直线A1B与AC所成角的余弦值;
(Ⅱ)要证AM⊥平面A1BC,只需证明直线AM垂直平面A1BC内的两条相交直线A1C、BC即可;
(Ⅲ)在三角形ABC中,作AB边上的高CH,垂足为H,连接MH,说明∠MHC是二面角M-AB-C的平面角,通过解三角形求二面角M-AB-C的正切值.
(Ⅱ)要证AM⊥平面A1BC,只需证明直线AM垂直平面A1BC内的两条相交直线A1C、BC即可;
(Ⅲ)在三角形ABC中,作AB边上的高CH,垂足为H,连接MH,说明∠MHC是二面角M-AB-C的平面角,通过解三角形求二面角M-AB-C的正切值.
解答: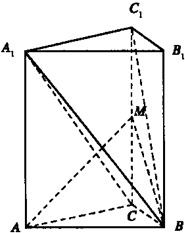 (Ⅰ)解:在直棱柱ABC-A1B1C1中,
(Ⅰ)解:在直棱柱ABC-A1B1C1中,
AC∥A1C1∴∠BA1C1是异面直线A1B
与AC所成的角(2分)
连接BC1
∴CC1⊥平面A1B1C1
∴CC1⊥A1C1
又∠A1C1B1=∠ACB=90°
即A1C1⊥B1C1
∴A1C1⊥平面BB1C1C
∴BC1?平面BB1C1C
∴A1C1⊥BC1
在直角三角形BCC1中,BC=1,CC1=AA1=
,∴BC1=
=
在直角三角形A1BC1中,A1C1=
,BC1=
∴A1B=
=
,∴cosBA1C1=
=
(4分)
(Ⅱ)证明:由(I)可知,BC⊥AC,BC⊥CC1
∴BC⊥平面ACC1A1,又AM?平面ACC1A1,则BC⊥AM
∵AM⊥A1C,∴AM⊥平面A1BC
(Ⅲ)解: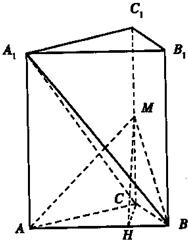
在三角形ABC中,作AB边上的高CH,垂足为H,连接MH,
显然CH是MH在平面ABC上的射影
∴MH⊥AB
∴∠MHC是二面角M-AB-C的平面角
(11分)
∵AM⊥A1C
∴∠MAC=∠AA1C,则
tanMAC=tanAA1C
即
=
,又AA1=
,AC=
∴MC=
又CH=
,故在直角三角形MCH中,tanMHC=
=
=
(13分)
 (Ⅰ)解:在直棱柱ABC-A1B1C1中,
(Ⅰ)解:在直棱柱ABC-A1B1C1中,AC∥A1C1∴∠BA1C1是异面直线A1B
与AC所成的角(2分)
连接BC1
∴CC1⊥平面A1B1C1
∴CC1⊥A1C1
又∠A1C1B1=∠ACB=90°
即A1C1⊥B1C1
∴A1C1⊥平面BB1C1C
∴BC1?平面BB1C1C
∴A1C1⊥BC1
在直角三角形BCC1中,BC=1,CC1=AA1=
| 6 |
BC2+C
|
| 7 |
在直角三角形A1BC1中,A1C1=
| 3 |
| 7 |
∴A1B=
A1
|
| 10 |
| A1C1 |
| A1B |
| ||
| 10 |
(Ⅱ)证明:由(I)可知,BC⊥AC,BC⊥CC1
∴BC⊥平面ACC1A1,又AM?平面ACC1A1,则BC⊥AM
∵AM⊥A1C,∴AM⊥平面A1BC
(Ⅲ)解:

在三角形ABC中,作AB边上的高CH,垂足为H,连接MH,
显然CH是MH在平面ABC上的射影
∴MH⊥AB
∴∠MHC是二面角M-AB-C的平面角
(11分)
∵AM⊥A1C
∴∠MAC=∠AA1C,则
tanMAC=tanAA1C
即
| AC |
| AA1 |
| MC |
| AC |
| 6 |
| 3 |
| ||
| 2 |
又CH=
| ||
| 2 |
| MC |
| CH |
| ||||
|
| 2 |
点评:本题考查直线与平面垂直的判定,二面角的求法,异面直线的夹角的求法,考查学生逻辑思维能力,计算能力,是中档题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目




