题目内容
【题目】某同学用“五点法”画函数![]() 在某一周期内的图像时,列表并填入的部分数据如下表:
在某一周期内的图像时,列表并填入的部分数据如下表:
|
|
|
|
|
|
| 0 |
|
|
|
|
| 0 | 1 | 0 |
| 0 |
| 0 |
| 0 |
| 0 |
(1)请写出上表的![]() 及函数
及函数![]() 的解析式;
的解析式;
(2)将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,再将所得图像上各点的横坐标缩小为原来的
个单位,再将所得图像上各点的横坐标缩小为原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]() 的图像,求
的图像,求![]() 的解析式及
的解析式及 的单调递增区间;
的单调递增区间;
(3)在(2)的条件下,若![]() 在
在![]() 上恰有奇数个零点,求实数
上恰有奇数个零点,求实数![]() 与零点个数
与零点个数![]() 的值.
的值.
【答案】(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
【解析】
(1)根据表中数据可得关于![]() 的方程组,解出
的方程组,解出![]() 的值后可得
的值后可得![]() 的值,再由表中数据可得
的值,再由表中数据可得![]() ,从而可得函数的解析式.
,从而可得函数的解析式.
(2)先求出![]() 的解析式,再求出
的解析式,再求出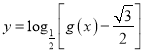 的定义域,结合三角函数的单调性可得复合函数的单调增区间.
的定义域,结合三角函数的单调性可得复合函数的单调增区间.
(3)令![]() ,设方程
,设方程![]() 的根为
的根为![]() ,分①
,分①![]() ;②
;②![]() ;③
;③![]() 三种情况讨论
三种情况讨论![]() 在
在![]() 及
及![]() 上零点个数,再根据周期性得到
上零点个数,再根据周期性得到![]() 的零点个数,结合题设条件可得
的零点个数,结合题设条件可得![]() 的值及相应的零点个数.
的值及相应的零点个数.
(1)根据表中的数据可得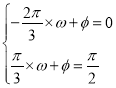 ,解得
,解得 ,
,
故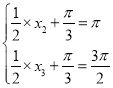 ,所以
,所以 ,又
,又![]() ,故
,故![]() .
.
所以![]() .
.
(2)将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,所得图像的解析式为:
个单位,所得图像的解析式为:
![]() ,
,
再将所得图像上各点的横坐标缩小为原来的![]() ,纵坐标不变,得到函数
,纵坐标不变,得到函数![]() 的图像,
的图像,
故![]() .
.
此时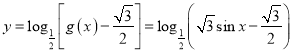 ,
,
令![]() ,则
,则![]() ,故
,故![]() .
.
当![]() 时,
时,![]() 为增函数,
为增函数,
故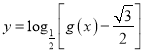 为减函数;
为减函数;
当![]() 时,
时,![]() 为减函数;
为减函数;
故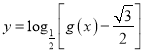 为增函数.
为增函数.
所以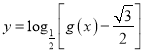 的增区间为
的增区间为![]() .
.
(3)![]() ,
,![]() 的周期为
的周期为![]() ,
,
当![]() 时,令
时,令![]() ,考虑方程
,考虑方程![]() 的根情况,
的根情况,
因![]() ,故
,故![]() 在
在![]() 必有两个不同的实数根
必有两个不同的实数根![]() ,
,
因为![]() 在
在![]() 有奇数个零点,故
有奇数个零点,故![]() 或
或![]() .
.
若![]() ,则方程
,则方程![]() 、
、![]() 在
在![]() 共有4个不同的实数根,
共有4个不同的实数根,
在![]() 有0个实数根或2个实数根,
有0个实数根或2个实数根,
故![]() 在
在![]() 有
有![]() 个根或
个根或![]() 个根,
个根,
与![]() 有奇数个零点矛盾,舍去.
有奇数个零点矛盾,舍去.
若![]() ,则
,则![]() 在
在![]() 共有2个不同的实数根,在
共有2个不同的实数根,在![]() 有0个实数根或2个实数根,
有0个实数根或2个实数根,
故![]() 在
在![]() 有
有
![]() 个根或
个根或![]() ,
,
与![]() 有奇数个零点矛盾,舍去.
有奇数个零点矛盾,舍去.
同理![]() 也不成立,所以
也不成立,所以![]() 或
或![]() ,
,
若![]() ,则
,则![]() ,
,![]() ,
,
方程![]() 、
、![]() 在
在![]() 共有3个不同的实数根,而在
共有3个不同的实数根,而在![]() 上,
上,![]() 有两个不同的根,
有两个不同的根,![]() 无解,
无解,
所以![]() 在
在![]() 有
有![]() 个根,符合要求;
个根,符合要求;
若![]() ,则
,则![]() ,
,![]() ,
,
方程![]() 、
、![]() 在
在![]() 共有3个不同的实数根,而在
共有3个不同的实数根,而在![]() 上,
上,![]() 无解,
无解,![]() 有一个根,
有一个根,
所以故![]() 在
在![]() 有
有![]() 个根,与题设矛盾,舍去.
个根,与题设矛盾,舍去.
综上,![]() ,
,![]() 在
在![]() 共有
共有![]() 个不同的零点.
个不同的零点.

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案