��Ŀ����
����Ŀ��ij֪��Ʒ����������������ϲ�������۸�ij�����������Ƴ�A��B��C���ַ��ڸ��ʽ���۸�Ʒ�����������Խ���100λ�����������ڸ���Ŀͻ�����ͳ�Ʒ������õ����µ���״ͼ����֪��A��B��C���ַ��ڸ��������У��þ�����ÿ���۴�Ʒ������1������õ�����ֱ���1��Ԫ��2��Ԫ��3��Ԫ���ּ������˴Ӹ����������̴��������������ڸ��ʽ�������Ʒ������һ��������100λ�ͻ������õķ��ڸ��ʽ��Ƶ�ʴ���1λ�ͻ�������Ӧ���ڸ��ʽ�ĸ��ʣ�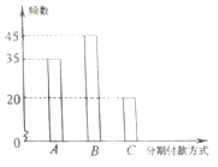
��1����������˲��ò�ͬ���ڸ��ʽ�ĸ��ʣ�
��2����X����λ����Ԫ��Ϊ�����������̴Ӽ������˹���������õ�������X�ķֲ�����������
���𰸡�
��1��
�⣺������ã�
P��A��= ![]() =0.35��P��B��=
=0.35��P��B��= ![]() =0.45��P��C��=
=0.45��P��C��= ![]() =0.2��
=0.2��
��������˲��ò�ͬ���ڸ��ʽ�ĸ��ʣ�
p=1��[P��A��P��A��+P��B��P��B��+P��C��P��C��]=0.635
��2��
�⣺��X����λ����Ԫ��Ϊ�����������̴Ӽ������˹���������õ�����
��X�Ŀ���ȡֵΪ2��3��4��5��6��
P��X=2��=P��A��P��A��=0.35��0.35=0.1225��
P��X=3��=P��A��P��B��+P��B��P��A��=0.35��0.45+0.45��0.35=0.315��
P��X=4��=P��A��P��C��+P��B��P��B��+P��C��P��A��=0.35��0.2+0.45��0.45+0.2��0.35=0.3425��
P��X=5��=P��B��P��C��+P��C��P��B��=0.45��0.2+0.2��0.45=0.18��
P��X=6��=P��C��P��C��=0.2��0.2=0.04��
��X�ķֲ���Ϊ��
X | 2 | 3 | 4 | 5 | 6 |
P | 0.1225 | 0.315 | 0.3425 | 0.18 | 0.04 |
E��X��=0.1225��2+0.315��3+0.3425��4+0.18��5+0.04��6=3.7
����������1��������ã�P��A��= ![]() =0.35��P��B��=
=0.35��P��B��= ![]() =0.45��P��C��=
=0.45��P��C��= ![]() =0.2�����ö����¼����ʼ��㹫ʽ������������˲��ò�ͬ���ڸ��ʽ�ĸ��ʣ���2����X����λ����Ԫ��Ϊ�����������̴Ӽ������˹���������õ�������X�Ŀ���ȡֵΪ2��3��4��5��6���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�E��X����
=0.2�����ö����¼����ʼ��㹫ʽ������������˲��ò�ͬ���ڸ��ʽ�ĸ��ʣ���2����X����λ����Ԫ��Ϊ�����������̴Ӽ������˹���������õ�������X�Ŀ���ȡֵΪ2��3��4��5��6���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к�E��X����

 ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�����Ŀ��ijͬѧ�á���㷨��������![]() ��ijһ�����ڵ�ͼ��ʱ���б�������IJ����������±���
��ijһ�����ڵ�ͼ��ʱ���б�������IJ����������±���
|
|
|
|
|
|
| 0 |
|
|
|
|
| 0 | 1 | 0 |
| 0 |
| 0 |
| 0 |
| 0 |
(1)��д���ϱ���![]() ������
������![]() �Ľ���ʽ��
�Ľ���ʽ��
(2)������![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ����λ���ٽ�����ͼ���ϸ���ĺ�������СΪԭ����
����λ���ٽ�����ͼ���ϸ���ĺ�������СΪԭ����![]() �������겻�䣬�õ�����
�������겻�䣬�õ�����![]() ��ͼ����
��ͼ����![]() �Ľ���ʽ��
�Ľ���ʽ�� �ĵ����������䣻
�ĵ����������䣻
(3)��(2)�������£���![]() ��
��![]() ��ǡ����������㣬��ʵ��
��ǡ����������㣬��ʵ��![]() ��������
��������![]() ��ֵ.
��ֵ.