题目内容
在等差数列 中,公差d >0,
中,公差d >0, 是方程
是方程 的两个根,
的两个根, 是数列
是数列 的前n项的和,那么满足条件
的前n项的和,那么满足条件 >0的最小自然数n=( )
>0的最小自然数n=( )
| A.4018 | B.4017 | C.2009 | D.2010 |
A
解析试题分析:由a2009,a2010是方程 x2-3x-5=0 的两个根,知a2009+a2010=3,a2009•a2010=-5,a2009,a2010符号相反,由d>0,知a2009<0,a2010>0,且|a2009|<|a2010|,由此能求出满足条件Sn>0的最大自然数n.解:∵a2009,a2010是方程 x2-3x-5=0 的两个根,∴a2009+a2010=3,a2009•a2010=-5,∴a2009,a2010符号相反,∵d>0,∴a2009<0,a2010>0,且|a2009|<|a2010|,∴S(2009×2)=S4018=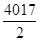 ×(a2009+a2010)=3×2009>0, S(2009×2-1)=S4017=
×(a2009+a2010)=3×2009>0, S(2009×2-1)=S4017=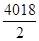 (a2009+a2009)=a2009×4017<0,所以Sn>0的最大n=4018.故选A.
(a2009+a2009)=a2009×4017<0,所以Sn>0的最大n=4018.故选A.
考点:数列与函数
点评:本题考查数列与函数的综合,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
正项等比数列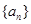 中,
中, 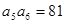 ,则
,则 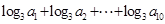 的值是( )
的值是( )
| A.2 | B.5 | C.10 | D.20 |
设数列 是等比数列,则“
是等比数列,则“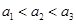 ”是数列
”是数列 是递增数列的
是递增数列的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知两个正数a,b的等差中项为4,则a,b的等比中项的最大值为( )
| A.2 | B.4 | C.8 | D.16 |
数列 为等比数列,且
为等比数列,且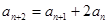 ,
,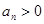 ,则该数列公比
,则该数列公比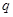 =( )
=( )
| A.1 | B.2 | C.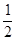 | D. |
等比数列 的前
的前 项和为
项和为 ,若
,若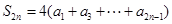 ,
,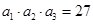 ,则
,则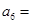 ( )
( )
A. | B. | C.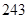 | D.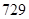 |
设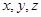 是不相等的三个数,则使
是不相等的三个数,则使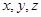 成等差数列, 且
成等差数列, 且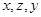 成等比数列的条件是( )
成等比数列的条件是( )
A.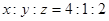 | B.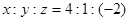 |
C.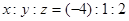 | D.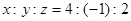 |
一个等比数列 的前n项和为48,前2n项和为60,则前3n项和为( )
的前n项和为48,前2n项和为60,则前3n项和为( )
| A.63 | B.108 | C.75 | D.83 |
 满足:
满足: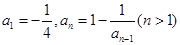 ,则
,则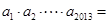 .
.