题目内容
【题目】已知在多面体![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 且平面
且平面![]() 平面
平面![]() .
.
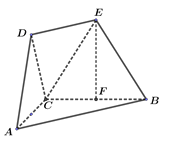
(1)设点![]() 为线段
为线段![]() 的中点,试证明
的中点,试证明![]() 平面
平面![]() ;
;
(2)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析(2)![]()
【解析】
(1)由四边形![]() 为平行四边形.∴
为平行四边形.∴![]() ,再结合
,再结合![]() 平面
平面![]() ,即可证明
,即可证明![]() 平面
平面![]() ;
;
(2)由空间向量的应用,建立以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 与
与![]() 平行的直线为
平行的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴的空间直角坐标系,再求出平面
轴的空间直角坐标系,再求出平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,再利用向量夹角公式求解即可.
,再利用向量夹角公式求解即可.
(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,
,
∵在![]() 中
中![]() ,∴
,∴![]() .
.
∴由平面![]() 平面
平面![]() ,且交线为
,且交线为![]() 得
得![]() 平面
平面![]() .
.
∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,∴
的中点,∴![]() ,且
,且![]() .
.
又![]() ,
,![]() ,∴
,∴![]() ,且
,且![]() .
.
∴四边形![]() 为平行四边形.∴
为平行四边形.∴![]() ,
,
∴![]() 平面
平面![]() .
.
(2)∵![]() 平面
平面![]() ,
,![]() ,
,
∴以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,过点
轴,过点![]() 与
与![]() 平行的直线为
平行的直线为![]() 轴,
轴,![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系.则
轴,建立空间直角坐标系.则![]() ,
,![]() ,
,![]() .
.
∵![]() 平面
平面![]() ,∴直线
,∴直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
∴![]() .∴
.∴![]() .
.
可取平面![]() 的法向量
的法向量![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,![]() ,
,![]() ,
,
则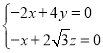 ,取
,取![]() ,则
,则![]() ,
,![]() .∴
.∴![]() ,
,
∴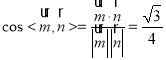 ,
,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案【题目】改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
仅使用A | 18人 | 9人 | 3人 |
仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
【题目】高铁是一种快捷的交通工具,为我们的出行提供了极大的方便。某高铁换乘站设有编号为①,②,③,④,⑤的五个安全出口,若同时开放其中的两个安全出口,疏散![]() 名乘客所需的时间如下:
名乘客所需的时间如下:
安全出口编号 | ①② | ②③ | ③④ | ④⑤ | ①⑤ |
疏散乘客时间(s) | 120 | 220 | 160 | 140 | 200 |
则疏散乘客最快的一个安全出口的编号是( )
A. ①B. ②C. ④D. ⑤