题目内容
13.下列命题中正确的个数是( )①对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R均有x2+x+1>0
②m=3是直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直的充要条件;
③已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为$\hat y$=1.23x+0.08
④若x>0,且x≠1,则lnx+$\frac{1}{lnx}$≥2.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用命题的否定判断①的正误;利用在垂直的充要条件判断②的正误;利用回归直线方程判断③的正误;利用好的值判断④的正误.
解答 解:对于①,对于命题p:?x∈R,使得x2+x+1<0,则¬p:?x∈R均有x2+x+1>0,不满足命题的否定,是①假命题.
对于②,m=3⇒直线(m+3)x+my-2=0与直线mx-6y+5=0互相垂直,但是直线垂直也可以得到m=0,命题判断为充要条件,不成立,所以②是假命题;
对于③,已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为$\hat y$=1.23x+0.08,正确,所以③是真命题;
对于④,若x>0,且x≠1,则lnx+$\frac{1}{lnx}$≥2.例如x=$\frac{1}{e}$,lnx+$\frac{1}{lnx}$=-2,显然④不正确,所以④是假命题.
故选:A.
点评 本题考查命题的真假的判断与应用,考查命题的否定、充要条件、基本不等式的应用,是基本题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.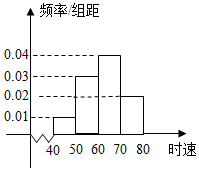 已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,估计这辆汽车在这段公路时速的众数是( )
已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,估计这辆汽车在这段公路时速的众数是( )
 已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,估计这辆汽车在这段公路时速的众数是( )
已知200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,估计这辆汽车在这段公路时速的众数是( )| A. | 60 | B. | 65 | C. | 60.5 | D. | 70 |
5.从某校高二年级随机抽取10名学生进行数学能力测试,成绩结果:68,81,79,81,90,86,74,84,69,78,设学生测试成绩的平均数和中位数,众数分别为a,b,c,则( )
| A. | a-b<c | B. | a<b-c | C. | a<b<c | D. | b<a<c |
2.从某5人中选派3人分别参加数学、物理、化学竞赛,每个学科各1人,其中甲、乙两人至多选1人参赛,则不同的参赛方案共有( )
| A. | 24种 | B. | 36种 | C. | 42种 | D. | 48种 |