题目内容
1.已知函数f(x)=$\left\{\begin{array}{l}{-x-2}&{(x≤-1)}\\{{x}^{2}-x-2}&{(-1<x≤2)}\\{x+2}&{(x>2)}\end{array}\right.$(1)请画出函数f(x)的图象;
(2)求f(1);
(3)求f[f(1)].
分析 (1)直接利用分段函数画出函数的图象即可.
(2)利用函数的解析式,求解函数值即可.
(3)由里及外逐步求解函数值即可.
解答 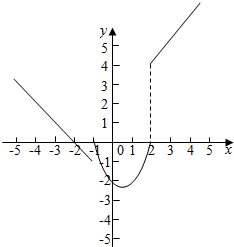 解:函数f(x)=$\left\{\begin{array}{l}{-x-2}&{(x≤-1)}\\{{x}^{2}-x-2}&{(-1<x≤2)}\\{x+2}&{(x>2)}\end{array}\right.$
解:函数f(x)=$\left\{\begin{array}{l}{-x-2}&{(x≤-1)}\\{{x}^{2}-x-2}&{(-1<x≤2)}\\{x+2}&{(x>2)}\end{array}\right.$
(1)函数f(x)的图象如图:;
(2)f(1)=12-1-2=-2;
(3)求f[f(1)]=f(-2)=2-2=0.
点评 本题考查分段函数的图象的画法,函数值的求法,考查计算能力以及作图能力.

练习册系列答案
相关题目
9.若函数f(x)在R上单调递增,则f(x2-2x)与f(-1)的大小关系为( )
| A. | f(x2-2x)≥f(-1) | B. | f(x2-2x)≤f(-1) | C. | f(x2-2x)=f(-1) | D. | 不能确定 |
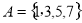 ,
,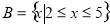 ,则
,则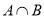 等于
等于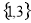 B.
B. 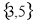 C.
C.  D.
D.