��Ŀ����
 A��ѡ��4-1������֤��ѡ��
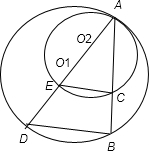
A��ѡ��4-1������֤��ѡ����ͼ��ԲO1��ԲO2�����ڵ�A����뾶�ֱ�Ϊr1��r2��r1��r2 ����ԲO1����AB��ԲO2�ڵ�C �� O1����AB�ϣ�����֤��AB��ACΪ��ֵ��
B��ѡ��4-2��������任
��֪����A=
|
|
| �� |
| �� |
| �� |
C��ѡ��4-4������ϵ���������
��ƽ��ֱ������ϵxOy�У������Բ
|
|
D��ѡ��4-5������ʽѡ������С������10�֣�
�ⲻ��ʽ��x+|2x-1|��3��
������A����ͼ������ EC��DB��AB��AC=AD��AE=2r1��2r2��֤�����ۣ�
B��������
=
���� A2
=
�����þ�������㷨���ô���ϵ�����ɵ�x �� y ��ֵ���Ӷ��������
��
C������Բ�IJ������̻�Ϊ��ͨ���̣�����ҽ�������꣬��ֱ�߲������̻�Ϊ��ͨ���̣����б�ʣ��õ�бʽ
�������ֱ�ߵķ��̣�
D��ԭ����ʽ�ɻ�Ϊ
����
���ֱ�������������ʽ��Ľ⼯��
�ٰѽ⼯ȡ������
B��������
| �� |
|
| �� |
| �� |
| �� |
C������Բ�IJ������̻�Ϊ��ͨ���̣�����ҽ�������꣬��ֱ�߲������̻�Ϊ��ͨ���̣����б�ʣ��õ�бʽ
�������ֱ�ߵķ��̣�
D��ԭ����ʽ�ɻ�Ϊ
|
|
�ٰѽ⼯ȡ������
����⣺A����ͼ������AO1���ӳ�������Բ��D��E����O2��AD�ϣ�����ֱ���Ե�Բ�ܽǵ���90��ɵã���ACE=��ABD=90�㣬
��EC��DB����AB��AC=AD��AE=2r1��2r2=r1��r2 Ϊ��ֵ��
B��A2=
=
��������
=
���� A2
=
�ɵ�
=
����
����� x=-1��y=2��
������
=
��
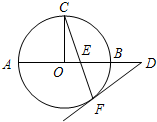
C����Բ
����Ϊ����������ͨ����Ϊ
+
=1���ҽ���Ϊ��4��0����
ֱ��
��tΪ������ �� x-2 y+2=0��б�ʵ���
���������ֱ�߷���Ϊ
y-0=
��x-4������ x-2 y-4=0��
D��ԭ����ʽ�ɻ�Ϊ
����
��
���
��x��
����-2��x��
���ʲ���ʽ�Ľ⼯Ϊ {x|-2��x��
}��
��EC��DB����AB��AC=AD��AE=2r1��2r2=r1��r2 Ϊ��ֵ��

B��A2=
|
|
|
| �� |
|
| �� |
| �� |
|
|
|
|
������
| �� |
|
C����Բ
|
| x2 |
| 25 |
| y2 |
| 9 |
ֱ��
|
| 1 |
| 2 |
y-0=
| 1 |
| 2 |
D��ԭ����ʽ�ɻ�Ϊ
|
|
���
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| 4 |
| 3 |
���������⿼��Բ��Բ��λ�ù�ϵ��������������ͨ���̵Ļ�������������㷨����ֵ����ʽ�Ľⷨ��

��ϰ��ϵ�д�
�����Ŀ
 A��ѡ��4-1������֤��ѡ����
A��ѡ��4-1������֤��ѡ���� ѡ���⣺��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣���20�֣����Ӧд������˵����֤�����̻����㲽�裮
ѡ���⣺��A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣���20�֣����Ӧд������˵����֤�����̻����㲽�裮 A��ѡ��4-1������֤��ѡ��
A��ѡ��4-1������֤��ѡ�� ѡ������A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣�
ѡ������A��B��C��D��С����ֻ��ѡ��2�⣬ÿС��10�֣�����20�֣� ��A��B��C��D�ĸ���ѡ��2��A��ѡ��4-1������֤��ѡ����
��A��B��C��D�ĸ���ѡ��2��A��ѡ��4-1������֤��ѡ����