题目内容
(本小题满分12分)
已知向量 与
与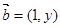 共线,且有函数
共线,且有函数
(Ⅰ)求函数 的周期与最大值;
的周期与最大值;
(Ⅱ)已知锐角DABC的三个内角分别是A、B、C,若有 ,边
,边 ,
, ,求AC的长.
,求AC的长.
(1)f(x)的周期为2π,函数的最大值为2;(2)2.
解析试题分析:∵向量 与
与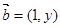 共线,
共线,
∴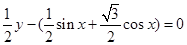 ,∴y=f(x)=
,∴y=f(x)=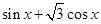 =2sin(
=2sin(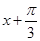 )
)
(Ⅰ)∵ω=1,∴T=2π,
∵-2≤2sin(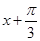 )≤2,s所以f(x)的周期为2π,函数的最大值为2;
)≤2,s所以f(x)的周期为2π,函数的最大值为2;
(Ⅱ)由 ,得2sin(
,得2sin(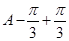 )=
)=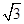 ,即sinA=
,即sinA= ,
,
∵ ,
, ,
,
∴由正弦定理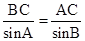 得:AC=
得:AC=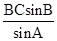 =2.
=2.
考点:本题主要考查平面向量的坐标运算,共线向量,两角和差的正弦,正弦函数的性质,正弦定理的应用。
点评:中档题,本题将平面向量、三角函数、正弦定理结合在一起进行考查,具有较强的综合性。本题解法体现的的是解答此类题的一般方法,如,研究三角函数的图象和性质,往往要先“化一”,研究三角形问题,往往利用正弦定理、余弦定理等等。

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
在四边形ABCD中, ,
, ,则四边形ABCD的面积为( )
,则四边形ABCD的面积为( )
A. | B. | C.2 | D.1 |
 ,
, ,-
,- <θ<
<θ< ,求θ;
,求θ; 的最大值.
的最大值. ,
, 的值; (2)求
的值; (2)求 的夹角
的夹角 ; (3)求
; (3)求 的值;
的值; =
= ,
, =
= ,
, 为锐角.
为锐角. ,求sin
,求sin 、
、 、
、
 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中 ,且
,且 ,求
,求 且
且 与
与 垂直,求
垂直,求 .
. 中,点
中,点 在线段
在线段 上,且
上,且 ,延长
,延长 到
到 ,使
,使 .设
.设 .
.
 表示向量
表示向量 ;
;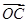 与
与 共线,求
共线,求 的值.
的值.  |=1,|
|=1,| |=
|= ;(I)若
;(I)若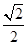 ,求
,求 与
与 的夹角;(II)若
的夹角;(II)若 ,求|
,求| ,
, .
. 和
和 ;
; 为何值时,
为何值时, .
.