题目内容
已知 是双曲线
是双曲线 的左右焦点,点
的左右焦点,点 关于渐近线的对称点恰落在以
关于渐近线的对称点恰落在以 为圆心,
为圆心, 为半径的圆上,则双曲线的离心率为( )
为半径的圆上,则双曲线的离心率为( )
A. | B. | C. | D. |
A
解析试题分析:如图所示,一方面: 关于渐近线对称的点
关于渐近线对称的点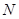 在圆
在圆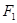 上,依题意有:
上,依题意有: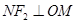 且
且 是线段
是线段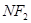 的中点,于是
的中点,于是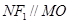 ,即有
,即有 ;另一方面:焦点
;另一方面:焦点 到渐近线的距离
到渐近线的距离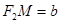 ,故
,故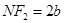 ,再加上
,再加上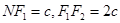 ,于是在
,于是在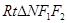 中由勾股定理可得
中由勾股定理可得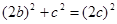 ,即
,即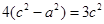 ,整理得
,整理得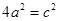 ,
,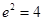 ,
,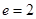 ,故选A.
,故选A.
考点:双曲线的标准方程及其几何性质.

练习册系列答案
相关题目
已知抛物线C: 的焦点为
的焦点为 ,
,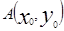 是C上一点,
是C上一点, ,则
,则 ( )
( )
| A. 1 | B. 2 | C. 4 | D. 8 |
已知双曲线 的一条渐近线方程为
的一条渐近线方程为 ,则双曲线离心率
,则双曲线离心率 =( )
=( )
A. | B. | C. | D. |
若抛物线 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
A. | B. | C. | D. |
曲线 在点
在点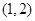 处的切线为
处的切线为 ,则直线
,则直线 上的任意点P与圆
上的任意点P与圆 上的任意点Q之间的最近距离是( )
上的任意点Q之间的最近距离是( )
A. | B. | C.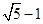 | D.2 |
[2014·蚌埠模拟]已知M(-2,0),N(2,0),|PM|-|PN|=4,则动点P的轨迹是( )
| A.双曲线 | B.双曲线左边一支 |
| C.一条射线 | D.双曲线右边一支 |
 、
、 是双曲线
是双曲线 (
( ,
, )的左右两个焦点,过点
)的左右两个焦点,过点 轴的直线与双曲线的两条渐近线分别交于
轴的直线与双曲线的两条渐近线分别交于 ,
, 两点,
两点,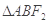 是锐角三角形,则该双曲线的离心率
是锐角三角形,则该双曲线的离心率 的取值范围是( )
的取值范围是( )



 =1的两个焦点,P是双曲线上的一点,且3|PF1|=4|PF2|,则△PF1F2的面积等于 ( )
=1的两个焦点,P是双曲线上的一点,且3|PF1|=4|PF2|,则△PF1F2的面积等于 ( )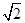

 的右焦点为F,若过点F且倾斜角为
的右焦点为F,若过点F且倾斜角为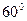 的直线与双曲线右支有且仅有一个交点,则此双曲线的离心率的取值范围是( )
的直线与双曲线右支有且仅有一个交点,则此双曲线的离心率的取值范围是( )


