题目内容
（2012•洛阳模拟）已知x1，x2是函数f(x)=e-x-|lnx|的两个零点，则（ ）
分析：若x1，x2是函数f(x)=e-x-|lnx|的两个零点，则x1，x2是函数y=e-x和y=|lnx|的图象交点的横坐标，在同一个坐标系中，画函数y=e-x和y=|lnx|的图象，利用对数函数的性质，可判断出x1x2的范围．
解答：解：若x1，x2是函数f(x)=e-x-|lnx|的两个零点，
则x1，x2是函数y=e-x和y=|lnx|的图象交点的横坐标
在同一个坐标系中，画函数y=e-x和y=|lnx|的图象如下图所示：
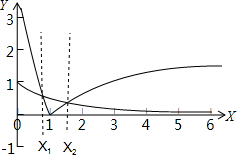
由图可得
即-1＜ln（x1•x2）＜1
即
＜x1•x2＜e
又∵-lnx1＞lnx2
∴ln（x1•x2）＜0
∴x1•x2＜1
综上
＜x1•x2＜1
故选A
则x1，x2是函数y=e-x和y=|lnx|的图象交点的横坐标
在同一个坐标系中，画函数y=e-x和y=|lnx|的图象如下图所示：
由图可得
|
即-1＜ln（x1•x2）＜1
即
| 1 |
| e |
又∵-lnx1＞lnx2
∴ln（x1•x2）＜0
∴x1•x2＜1
综上
| 1 |
| e |
故选A
点评：本题考查的知识点是函数的零点，对数函数的图象和性质，其中画出函数的图象，并利用数形结合的办法进行解答是关键．
练习册系列答案
相关题目
（2012•洛阳模拟）阅读如图的算法框图，输出的结果S的值为（ ）