题目内容
17.命题“?n∈N*,f(n)∈N*且f(n)≤n”的否定形式是( )| A. | ?n∈N*,f(n)∉N*且f(n)>n | B. | ?n∈N*,f(n)∉N*或f(n)>n | ||
| C. | ?n0∈N*,f(n0)∉N*且f(n0)>n0 | D. | ?n0∈N*,f(n0)∉N*或f(n0)>n0 |
分析 根据全称命题的否定是特称命题即可得到结论.
解答 解:命题为全称命题,
则命题的否定为:?n0∈N*,f(n0)∉N*或f(n0)>n0,
故选:D.
点评 本题主要考查含有量词的命题的否定,比较基础.

练习册系列答案
相关题目
7.二项式(x+1)n(n∈N+)的展开式中x2的系数为15,则n=( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
5.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1 (a>0,b>0)的一条渐近线过点(2,$\sqrt{3}$),且双曲线的一个焦点在抛物线y2=4$\sqrt{7}$x的准线上,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{21}$-$\frac{{y}^{2}}{28}$=1 | B. | $\frac{{x}^{2}}{28}$-$\frac{{y}^{2}}{21}$=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1 |
9.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的年宣传费xi和年销售量yi(i=1,2,…,8)数据作了初步处理,得到下面的散点图及一些统计量的值.
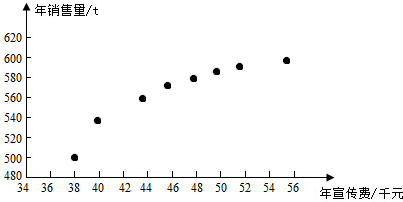
表中wi=$\sqrt{x}$i,$\overline{w}$=$\frac{1}{8}$$\sum _{i=1}^{8}w{\;}_{i}$
(Ⅰ)根据散点图判断,y=a+bx与y=c+d$\sqrt{x}$哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(i)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii)年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据(u1 v1),(u2 v2)…..(un vn),其回归线v=α+βu的斜率和截距的最小二乘估计分别为:$\widehat{β}$=$\frac{\sum_{i=1}^{n}({u}_{1}-\overline{u})({v}_{1}-\overline{v})}{\sum_{i=1}^{n}({u}_{1}-\overline{u})^{2}}$,$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$.

| $\overline{x}$ | $\overline{y}$ | $\overline{w}$ | $\sum _{i=1}^{8}$(xi-$\overline{x}$)2 | $\sum _{i=1}^{8}$(wi-$\overline{w}$)2 | $\sum _{i=1}^{8}$(xi-$\overline{x}$)(yi-$\overline{y}$) | $\sum _{i=1}^{8}$(wi-$\overline{w}$)(yi-$\overline{y}$) |
| 46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
(Ⅰ)根据散点图判断,y=a+bx与y=c+d$\sqrt{x}$哪一个适宜作为年销售量y关于年宣传费x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y-x.根据(Ⅱ)的结果回答下列问题:
(i)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii)年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据(u1 v1),(u2 v2)…..(un vn),其回归线v=α+βu的斜率和截距的最小二乘估计分别为:$\widehat{β}$=$\frac{\sum_{i=1}^{n}({u}_{1}-\overline{u})({v}_{1}-\overline{v})}{\sum_{i=1}^{n}({u}_{1}-\overline{u})^{2}}$,$\widehat{α}$=$\overline{v}$-$\widehat{β}$$\overline{u}$.
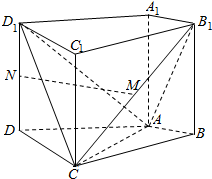 如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和D1D的中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=$\sqrt{5}$,且点M和N分别为B1C和D1D的中点.