题目内容
7.计算下列各式:(1)$(\frac{36}{49})^{\frac{1}{2}}$;
(2)2$\sqrt{3}$×$\root{3}{1.5}$×$\root{6}{12}$;
(3)${a}^{\frac{1}{2}}•{a}^{\frac{1}{4}}$$•{a}^{-\frac{1}{8}}$;
(4)2${x}^{-\frac{1}{3}}$($\frac{1}{2}$${x}^{\frac{1}{3}}$-2${x}^{-\frac{2}{3}}$)
分析 利用分数指数幂的运算法则即可得出.
解答 解:(1)$(\frac{36}{49})^{\frac{1}{2}}$=$(\frac{6}{7})^{2×\frac{1}{2}}$=$\frac{6}{7}$;
(2)2$\sqrt{3}$×$\root{3}{1.5}$×$\root{6}{12}$=$2×\root{6}{{3}^{3}×(\frac{3}{2})^{2}×12}$=2×3=6;
(3)${a}^{\frac{1}{2}}•{a}^{\frac{1}{4}}$$•{a}^{-\frac{1}{8}}$=${a}^{\frac{1}{2}+\frac{1}{4}-\frac{1}{8}}$=${a}^{\frac{5}{8}}$;
(4)2${x}^{-\frac{1}{3}}$($\frac{1}{2}$${x}^{\frac{1}{3}}$-2${x}^{-\frac{2}{3}}$)=$(2×\frac{1}{2})$${x}^{-\frac{1}{3}+\frac{1}{3}}$-$(2×2){x}^{-\frac{1}{3}-\frac{2}{3}}$=1-4x-1.
点评 本题考查了分数指数幂的运算法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
17.已知x=$\frac{π}{3}$是函数f(x)=(b-$\sqrt{3}a$)sinx+(a-b)cosx(a≠0)的一个零点,则函数g(x)=asinx-bcosx的图象可能是( )
| A. | 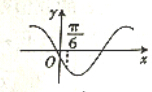 | B. | 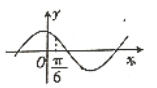 | ||
| C. | 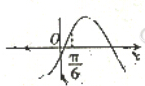 | D. | 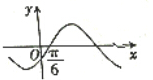 |
18.函数f(x)=ax与g(x)=-x+a的图象大致是( )
| A. | 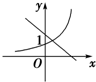 | B. | 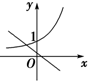 | C. | 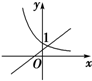 | D. | 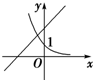 |
12. 如图所示,目标函数z=kx-y的可行域为四边形OABC,点B(3,2)是目标函数最优解,则k的取值范围( )
如图所示,目标函数z=kx-y的可行域为四边形OABC,点B(3,2)是目标函数最优解,则k的取值范围( )
 如图所示,目标函数z=kx-y的可行域为四边形OABC,点B(3,2)是目标函数最优解,则k的取值范围( )
如图所示,目标函数z=kx-y的可行域为四边形OABC,点B(3,2)是目标函数最优解,则k的取值范围( )| A. | ($\frac{2}{3}$,2) | B. | (1,$\frac{5}{3}$) | C. | (-2,-$\frac{2}{3}$) | D. | (-3,-$\frac{4}{3}$) |
19.已知f($\frac{2}{x}$+1)=2x+3,则f(5)=( )
| A. | 4 | B. | 2 | C. | 7 | D. | 5 |