题目内容
(本题满分14分)已知x=1是函数f(x)=mx![]() -3(m+1)x
-3(m+1)x![]() +nx+1的一个极值点,其中m、n∈R, m<0.(1)求m与n的关系表达式;(2)求f (x)的单调区间;(3)当x∈[-1,1]时,函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
+nx+1的一个极值点,其中m、n∈R, m<0.(1)求m与n的关系表达式;(2)求f (x)的单调区间;(3)当x∈[-1,1]时,函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
(Ⅰ) n=3m+6. (Ⅱ) 略(Ⅲ)-![]() <m<0.
<m<0.
解析:
(1)f′(x)=3mx![]() -6(m+1)x+n.因为x=1是f (x)的一个极值点,所以f′(1)=0,即3m-6(m+1)+n=0,
-6(m+1)x+n.因为x=1是f (x)的一个极值点,所以f′(1)=0,即3m-6(m+1)+n=0,
所以f′(1)=0.即3m-6(m+1)+n=0,所以n=3m+6.
(2)由(1)知,f′(x)=3mx![]() -6(m+1)x+3m+6=3m(x-1)[x-(1-
-6(m+1)x+3m+6=3m(x-1)[x-(1-![]() )].
)].
(ⅰ)当m<0时,有1>1+![]() ,当x变化时,f(x)与f′(x)的变化如下表:
,当x变化时,f(x)与f′(x)的变化如下表:
| X |
|
|
| 1 | (1,+ |
| f′(x) | <0 | 0 | >0 | 0 | <0 |
| f(x) | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
由上表知,当m<0时,f(x)在(-∞,1+![]() )单调递减,在(1+
)单调递减,在(1+![]() ,1)单调递增,在(1,+∞)单调递减.
,1)单调递增,在(1,+∞)单调递减.
(3)解法一:由已知,得f′(x)>3m,即mx![]() -2(m+1)x+2>0.
-2(m+1)x+2>0.
∵m<0,∴x![]() -
-![]() (m+1)x+
(m+1)x+![]() <0. 即x
<0. 即x![]() -2(1+
-2(1+![]() )x+
)x+![]() <0,x∈[-1,1].(*)
<0,x∈[-1,1].(*)
设g(x)=x![]() -2(1+
-2(1+![]() )x+
)x+![]() ,其函数图象的开口向上.
,其函数图象的开口向上.
由题意(*)式恒成立.∴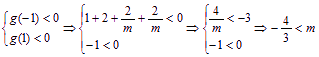 ,又m<0.
,又m<0.
∴-![]() <m<0.即m的取值范围是-
<m<0.即m的取值范围是-![]() <m<0.
<m<0.
解法二:由已知,得f′(x)>3m, 即3m(x-1)[x-(1+![]() )]>3m.∵m<0,∴(x-1)
)]>3m.∵m<0,∴(x-1)![]() <1(*)
<1(*)
(ⅰ)x=1时(*)式化成0<1恒成立,∴m<0.(ⅱ)x≠1时,∵x∈[-1,1],∴-2≤x-1<0.
(*)式化为![]() <(x-1)-
<(x-1)-![]() ,令t=x-1,则t∈[-2,0],记g(t)=t-
,令t=x-1,则t∈[-2,0],记g(t)=t-![]() ,则g(t)在区间[-2,0]是单调增函数.
,则g(t)在区间[-2,0]是单调增函数.
∴g(t)![]() =g(-2)=-2-
=g(-2)=-2-![]() =-
=-![]() .由(*)式恒成立,必有
.由(*)式恒成立,必有![]() <-
<-![]()
![]() -
-![]() <m,又m<0.∴-
<m,又m<0.∴-![]() <m<0.
<m<0.
综合(ⅰ)(ⅱ)知-![]() <m<0.
<m<0.


 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
