Question

（2011•嘉定区三模）已知函数f(x)=

|log4x|，0＜x≤4 - 1 4 x+2，x＞4

，若a、b、c的值互不相等，且f（a）=f（b）=f（c），则abc的取值范围是（　　）

A．（1，4）

B．（2，5）

C．（3，6）

D．（4，8）

Answer 1

分析：根据f（a）=f（b）=f（c），不妨a＜b＜c，然后画出函数f（x）分段函数中各部分的图象，再结合图象即可求出实数abc的范围．

解答：解：作出函数f（x）=

|log4x|，0＜x≤4 - 1 4 x+2，x＞4

的图象如图，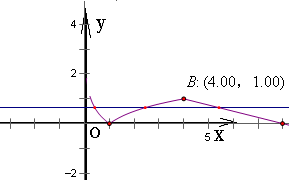
不妨设a＜b＜c，则
-log₄a=log₄b=-

1

4

c+2∈（0，1）
∴ab=1，0＜-

1

4

c+2＜1，
则abc=c∈（4，8）．
故选D．

点评：本题主要考查分段函数、对数的运算性质以及利用数形结合解决问题的能力．利用函数的图象交点研究方程的根的问题，是解答本题的关键．