题目内容
(本小题满分12分)四棱锥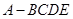 中,底面
中,底面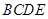 为矩形,侧面
为矩形,侧面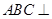 底面
底面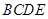 ,
,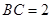 ,
,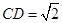 ,
, .
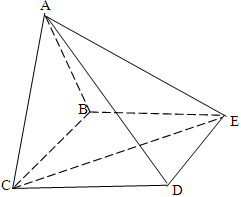
.
(Ⅰ)证明: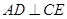 ;
;
(Ⅱ)设 与平面
与平面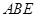 所成的角为
所成的角为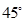 ,
,
求二面角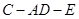 的余弦值.
的余弦值.
(I)见解析;(II)二面角C-AD-E的余弦值为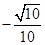 。
。
解析

练习册系列答案
相关题目
题目内容
(本小题满分12分)四棱锥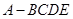 中,底面
中,底面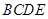 为矩形,侧面
为矩形,侧面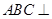 底面
底面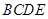 ,
,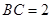 ,
,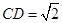 ,
, .
.
(Ⅰ)证明: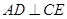 ;
;
(Ⅱ)设 与平面
与平面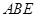 所成的角为
所成的角为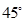 ,
,
求二面角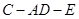 的余弦值.
的余弦值.
(I)见解析;(II)二面角C-AD-E的余弦值为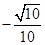 。
。
解析
