��Ŀ����
��֪����A={a1��a2������an}��1��a1��a2������an��n��2����������P���������i��j��1��i��j��n����aiaj��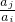 ������������һ������A��
������������һ������A��
��1���ֱ��ж�����{1��3��4}��{1��2��3��6}�Ƿ��������P����˵�����ɣ�
��2����a1��ֵ����n=3ʱ������a1��a2��a3�Ƿ�ɵȱ����У���˵�����ɣ�
��3���ɣ�2����ͨ����A��̽������д����������a1��a2������an��һ�������⣬������֤����
�⣺��1������3��4 �� ������������{1��3��4}��������{1��3��4} ����������P ��2��
������������{1��3��4}��������{1��3��4} ����������P ��2��
����1��2��1��3��1��6��2��3��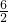 ��
�� ��
��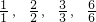 ����������{1��2��3��6}��
����������{1��2��3��6}��
������{1��2��3��6} ��������P��4��
��2����A={a1��a2������an} ��������P��
��anan ��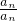 ��������һ������A������ 1��a1��a2����an����anan∉A ��5��
��������һ������A������ 1��a1��a2����an����anan∉A ��5��
�Ӷ�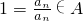 ��6�֡�a1=1 ��7��
��6�֡�a1=1 ��7��
��n=3 ʱ����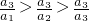 ��a1=1��a2a3∉A����
��a1=1��a2a3∉A����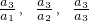 ������A ��8��
������A ��8��
�Ӷ�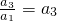 ��
��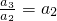 ��
��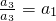 ����a3=a1a3=a22����9��
����a3=a1a3=a22����9��
������a1��a2��a3 �ɵȱ����С�10��
��3������һ�д��ڻ����3������n����������P ������a1��a2������an �ɵȱ����У� ��12��
֤�����ɣ�2����������n=2k+1��k��N��k��2����������a2k+1ai∉A��i=1����2k����֪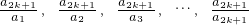 ������A����
������A����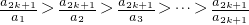 ���Ӷ�����
���Ӷ����� 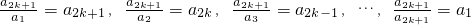 ���� a2k+1=a1a2k+1=a2a2k=a3a2k-1=��=ai+2a2k-i=��=a2ak+2=ak+12 �����~�� ��Ϊai+ja2k-i��ai+2a2k-i=a2k+1��0��i��k-2��3��j��2k-2i�������ԣ�ֻ��
���� a2k+1=a1a2k+1=a2a2k=a3a2k-1=��=ai+2a2k-i=��=a2ak+2=ak+12 �����~�� ��Ϊai+ja2k-i��ai+2a2k-i=a2k+1��0��i��k-2��3��j��2k-2i�������ԣ�ֻ��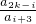 ��
��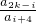 ��
��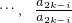 ������A�� ��i ��0 ��k-2 �о٣���õ���
������A�� ��i ��0 ��k-2 �о٣���õ���
��1�飺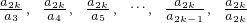 ����2k-2 �
����2k-2 �
��2�飺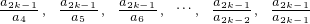 ����2k-4 �
����2k-4 �
��3�飺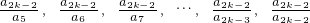 ����2k-6 �
����2k-6 �
����k-1 �飺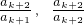 ����2 ���һ��ĵ�2���ܴ�����һ��ĵ�1�
����2 ���һ��ĵ�2���ܴ�����һ��ĵ�1�
��ע�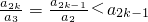 ���ʵ�1��ĸ�������������Ϊ��a2k-2��a2k-3��a2k-4������a2��a1����2��ĸ�������������Ϊ��a2k-4��a2k-5��a2k-6������a2��a1����3��ĸ�������������Ϊ��a2k-6��a2k-7��a2k-8������a2��a1�� ����k-1 ��ĸ�������������Ϊ��a2��a1�����ǣ���
���ʵ�1��ĸ�������������Ϊ��a2k-2��a2k-3��a2k-4������a2��a1����2��ĸ�������������Ϊ��a2k-4��a2k-5��a2k-6������a2��a1����3��ĸ�������������Ϊ��a2k-6��a2k-7��a2k-8������a2��a1�� ����k-1 ��ĸ�������������Ϊ��a2��a1�����ǣ���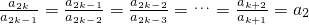 ���ɣ��~����
���ɣ��~����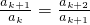 ��
��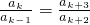 ������
������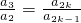 ����
����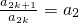 ��������a1��a2������an �ɵȱ����У���15��
��������a1��a2������an �ɵȱ����У���15��
��������1����������P���������i��j��1��i��j��n����aiaj��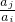 ������������һ������A����֤���ļ��ϼ�{1��3��4}��{1��2��3��6}�е��κ�����Ԫ�صĻ����Ƿ�Ϊ�ü����е�Ԫ�أ�
������������һ������A����֤���ļ��ϼ�{1��3��4}��{1��2��3��6}�е��κ�����Ԫ�صĻ����Ƿ�Ϊ�ü����е�Ԫ�أ�
��2������A={a1��a2������an} ��������P����anan ��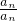 ��������һ������A������ 1��a1��a2����an����anan∉A �Ӷ�
��������һ������A������ 1��a1��a2����an����anan∉A �Ӷ�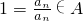 ���a1��ֵ����֤
���a1��ֵ����֤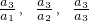 ������A���Ӷ�
������A���Ӷ�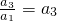 ��
��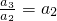 ��
��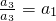 ����a3=a1a3=a22������ȱ����еĶ��壻
����a3=a1a3=a22������ȱ����еĶ��壻
��3������һ�д��ڻ����3������n����������P ������a1��a2������an �ɵȱ����У��ɣ�2����������n=2k+1��k��N��k��2����������a2k+1ai∉A��i=1����2k�������գ�2���ķ�������֤�����ɣ�
������������Ҫ���鼯�ϡ��ȱ����е����ʣ���������������������֤�������ַ������۵���ѧ˼�뷽���������ܺܺõĿ���ѧ����Ӧ��֪ʶ�������������������������ڶ������Ŀ��飬���ڽ��Ѳ���⣮
 ������������{1��3��4}��������{1��3��4} ����������P ��2��
������������{1��3��4}��������{1��3��4} ����������P ��2�� ����1��2��1��3��1��6��2��3��
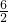 ��
��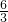 ��
��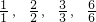 ����������{1��2��3��6}��
����������{1��2��3��6}��������{1��2��3��6} ��������P��4��
��2����A={a1��a2������an} ��������P��
��anan ��
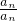 ��������һ������A������ 1��a1��a2����an����anan∉A ��5��
��������һ������A������ 1��a1��a2����an����anan∉A ��5�� �Ӷ�
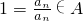 ��6�֡�a1=1 ��7��
��6�֡�a1=1 ��7�� ��n=3 ʱ����
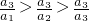 ��a1=1��a2a3∉A����
��a1=1��a2a3∉A����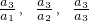 ������A ��8��
������A ��8���Ӷ�
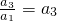 ��
��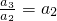 ��
��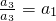 ����a3=a1a3=a22����9��
����a3=a1a3=a22����9��������a1��a2��a3 �ɵȱ����С�10��
��3������һ�д��ڻ����3������n����������P ������a1��a2������an �ɵȱ����У� ��12��
֤�����ɣ�2����������n=2k+1��k��N��k��2����������a2k+1ai∉A��i=1����2k����֪
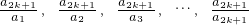 ������A����
������A����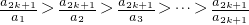 ���Ӷ�����
���Ӷ����� 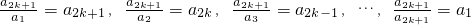 ���� a2k+1=a1a2k+1=a2a2k=a3a2k-1=��=ai+2a2k-i=��=a2ak+2=ak+12 �����~�� ��Ϊai+ja2k-i��ai+2a2k-i=a2k+1��0��i��k-2��3��j��2k-2i�������ԣ�ֻ��
���� a2k+1=a1a2k+1=a2a2k=a3a2k-1=��=ai+2a2k-i=��=a2ak+2=ak+12 �����~�� ��Ϊai+ja2k-i��ai+2a2k-i=a2k+1��0��i��k-2��3��j��2k-2i�������ԣ�ֻ��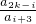 ��
��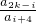 ��
��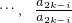 ������A�� ��i ��0 ��k-2 �о٣���õ���
������A�� ��i ��0 ��k-2 �о٣���õ�����1�飺
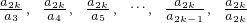 ����2k-2 �
����2k-2 ���2�飺
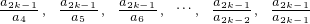 ����2k-4 �
����2k-4 ���3�飺
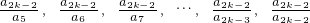 ����2k-6 �
����2k-6 � ����k-1 �飺
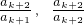 ����2 ���һ��ĵ�2���ܴ�����һ��ĵ�1�
����2 ���һ��ĵ�2���ܴ�����һ��ĵ�1���ע�
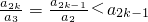 ���ʵ�1��ĸ�������������Ϊ��a2k-2��a2k-3��a2k-4������a2��a1����2��ĸ�������������Ϊ��a2k-4��a2k-5��a2k-6������a2��a1����3��ĸ�������������Ϊ��a2k-6��a2k-7��a2k-8������a2��a1�� ����k-1 ��ĸ�������������Ϊ��a2��a1�����ǣ���
���ʵ�1��ĸ�������������Ϊ��a2k-2��a2k-3��a2k-4������a2��a1����2��ĸ�������������Ϊ��a2k-4��a2k-5��a2k-6������a2��a1����3��ĸ�������������Ϊ��a2k-6��a2k-7��a2k-8������a2��a1�� ����k-1 ��ĸ�������������Ϊ��a2��a1�����ǣ���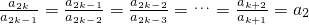 ���ɣ��~����
���ɣ��~����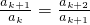 ��
��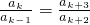 ������
������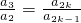 ����
����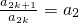 ��������a1��a2������an �ɵȱ����У���15��
��������a1��a2������an �ɵȱ����У���15����������1����������P���������i��j��1��i��j��n����aiaj��
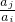 ������������һ������A����֤���ļ��ϼ�{1��3��4}��{1��2��3��6}�е��κ�����Ԫ�صĻ����Ƿ�Ϊ�ü����е�Ԫ�أ�
������������һ������A����֤���ļ��ϼ�{1��3��4}��{1��2��3��6}�е��κ�����Ԫ�صĻ����Ƿ�Ϊ�ü����е�Ԫ�أ���2������A={a1��a2������an} ��������P����anan ��
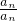 ��������һ������A������ 1��a1��a2����an����anan∉A �Ӷ�
��������һ������A������ 1��a1��a2����an����anan∉A �Ӷ�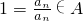 ���a1��ֵ����֤
���a1��ֵ����֤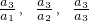 ������A���Ӷ�
������A���Ӷ�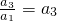 ��
��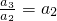 ��
��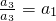 ����a3=a1a3=a22������ȱ����еĶ��壻
����a3=a1a3=a22������ȱ����еĶ��壻��3������һ�д��ڻ����3������n����������P ������a1��a2������an �ɵȱ����У��ɣ�2����������n=2k+1��k��N��k��2����������a2k+1ai∉A��i=1����2k�������գ�2���ķ�������֤�����ɣ�
������������Ҫ���鼯�ϡ��ȱ����е����ʣ���������������������֤�������ַ������۵���ѧ˼�뷽���������ܺܺõĿ���ѧ����Ӧ��֪ʶ�������������������������ڶ������Ŀ��飬���ڽ��Ѳ���⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ