题目内容
3.在长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=2,E,F分别是A1B1和B1C1的中点,则异面直线AE与BF所成的角.( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
分析 如图所示,建立空间直角坐标系.利用向量的夹角公式即可得出.
解答 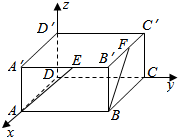 解:如图所示,建立空间直角坐标系.A(4,0,0),B(4,4,0),E(4,2,2),F(2,4,2).
解:如图所示,建立空间直角坐标系.A(4,0,0),B(4,4,0),E(4,2,2),F(2,4,2).
∴$\overrightarrow{AE}$=(0,2,2),$\overrightarrow{BF}$=(-2,0,2).
∴$cos<\overrightarrow{AE},\overrightarrow{BF}>$=$\frac{\overrightarrow{AE}•\overrightarrow{BF}}{|\overrightarrow{AE}||\overrightarrow{BF}|}$=$\frac{4}{\sqrt{4+4}\sqrt{4+4}}$=$\frac{1}{2}$.
∴异面直线AE与BF所成的角是60°.
故选:B.
点评 本题考查了利用向量夹角公式求异面直线所成的夹角方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
6.下列说法正确的是( )
| A. | log0.56>log0.54 | B. | 0.60.5>log0.60.5 | ||
| C. | 2.50<${(\frac{1}{2})^{2.5}}$ | D. | 90.9>270.48 |
18.观察下列各式:a1+b1+c1=2,a2+b2+c2=3,a3+b3+c3=5,a4+b4+c4=8,a5+b5+c5=13…,则a10+b10+c10=( )
| A. | 89 | B. | 144 | C. | 233 | D. | 232 |
15.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+\frac{1}{2}x(x<0)}\\{ln(x+1)(x≥0)}\end{array}\right.$,若函数y=f(x)-kx有3个零点,则实数k的取值范围为( )
| A. | $(0,\frac{1}{2})$ | B. | $(\frac{1}{2},1)$ | C. | (1,+∞) | D. | $(\frac{1}{4},1)$ |