题目内容
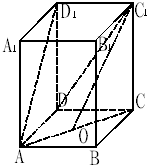 在长方体ABCD-A1B1C1D1中,AB=3,BC=AA1=4,点O是AC的中点.
在长方体ABCD-A1B1C1D1中,AB=3,BC=AA1=4,点O是AC的中点.(1)求证:AD1∥平面DOC1;
(2)求异面直线AD1和DC1所成角的余弦值.
分析:(1)连接CD1交C1D于点E,连接OE,由E是CD1中点,O是AC中点,知OE∥AD1,由此能证明AD1∥平面DOC1.
(2)连接BC1,BD,由E是PC中点,知EG∥DP.在长方体ABCD-A1B1C1D1中,由AB∥A1B1∥C1D1,AB=A1B1=C1D1,知四边形ABC1D1是平行四边形,所以∠BC1D或其补角为异面直线AD与C1D所成的角,由此能求出异面直线AD1与C1D所成的角的余弦值.
(2)连接BC1,BD,由E是PC中点,知EG∥DP.在长方体ABCD-A1B1C1D1中,由AB∥A1B1∥C1D1,AB=A1B1=C1D1,知四边形ABC1D1是平行四边形,所以∠BC1D或其补角为异面直线AD与C1D所成的角,由此能求出异面直线AD1与C1D所成的角的余弦值.
解答:(1)证明:连接CD1交C1D于点E,连接OE
∵E是CD1中点,O是AC中点∴OE∥AD1
又∵OE?平面DOC1,AD1?平面DOC1
∴AD1∥平面DOC1…(6分)
(2)解:连接BC1,BD
∵E是PC中点∴EG∥DP在长方体ABCD-A1B1C1D1中,AB∥A1B1∥C1D1,AB=A1B1=C1D1
∴四边形ABC1D1是平行四边形
∴BC1∥AD1
∴∠BC1D或其补角为异面直线AD与C1D所成的角…(3分)
在△BC1D中,BC1=4
,C1D=5,BD=5,
∴cos∠BC1D=
,
∴异面直线AD1与C1D所成的角的余弦值为
.…(3分)
∵E是CD1中点,O是AC中点∴OE∥AD1
又∵OE?平面DOC1,AD1?平面DOC1
∴AD1∥平面DOC1…(6分)
(2)解:连接BC1,BD
∵E是PC中点∴EG∥DP在长方体ABCD-A1B1C1D1中,AB∥A1B1∥C1D1,AB=A1B1=C1D1
∴四边形ABC1D1是平行四边形
∴BC1∥AD1
∴∠BC1D或其补角为异面直线AD与C1D所成的角…(3分)
在△BC1D中,BC1=4
| 2 |
∴cos∠BC1D=
2
| ||
| 5 |
∴异面直线AD1与C1D所成的角的余弦值为
2
| ||
| 5 |
点评:本题考查直线与平面平行的证明,考查异面直线所成角的余弦值的求法,解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在长方体ABCD-A'B'C'D'中,AB=
在长方体ABCD-A'B'C'D'中,AB= 如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比.
如图,在长方体ABCD-A′B′C′D′中,用截面截下一个棱锥C-A′DD′,求棱锥C-A′DD′的体积与剩余部分的体积之比. (2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离.
(2013•上海) 如图,在长方体ABCD-A′B′C′D′中,AB=2,AD=1,AA′=1.证明直线BC′平行于平面D′AC,并求直线BC′到平面D′AC的距离. (2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1.
(2009•青浦区二模)(理)在长方体ABCD-A'B'C'D'中,AB=2,AD=1,AA'=1. 已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.
已知在长方体ABCD-A′B′C′D′中,点E为棱CC′上任意一点,AB=BC=2,CC′=1.