题目内容
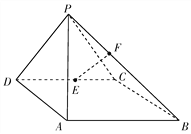
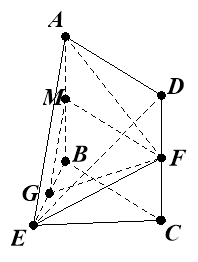
【题目】如图,在几何体ABCDE中,四边形ABCD是矩形,AB![]() 平面BEC,BE
平面BEC,BE![]() EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
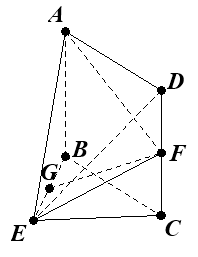
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求平面AEF与平面BEC所成锐二面角的余弦值.
【答案】(Ⅰ)详见解析;(Ⅱ) ![]() .
.
【解析】解法一:(Ⅰ)如图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,![]() ,又G是BE的中点,
,又G是BE的中点,![]() ,
,
又F是CD中点,![]() ,由四边形ABCD是矩形得,
,由四边形ABCD是矩形得,![]() ,所以
,所以![]() .从而四边形
.从而四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,,又
,,又![]() ,所以
,所以![]() .
.
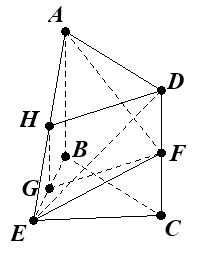

(Ⅱ)如图,在平面BEC内,过点B作![]() ,因为
,因为![]() .
.
又因为AB![]() 平面BEC,所以AB
平面BEC,所以AB![]() BE,AB
BE,AB![]() BQ
BQ
以B为原点,分别以![]() 的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,则A(0,0,2),B(0,0,0),E(2,0,0),F(2,2,1).因为AB
的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,则A(0,0,2),B(0,0,0),E(2,0,0),F(2,2,1).因为AB![]() 平面BEC,所以
平面BEC,所以![]() 为平面BEC的法向量,
为平面BEC的法向量,
设![]() 为平面AEF的法向量.又
为平面AEF的法向量.又![]()
由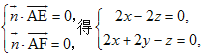 取
取![]() 得
得![]() .
.
从而![]()
所以平面AEF与平面BEC所成锐二面角的余弦值为![]() .
.
解法二:(Ⅰ)如图,取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,又
,又![]() 是
是![]() 的中点,可知
的中点,可知![]() ,
,
又![]() 面
面![]() ,
,![]() 面
面![]() ,所以
,所以![]() 平面
平面![]() .
.
在矩形ABCD中,由M,F分别是AB,CD的中点得![]() .
.
又![]() 面
面![]() ,
,![]() 面
面![]() ,所以
,所以![]() 面
面![]() .
.
又因为![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ,
,
所以面![]() 平面
平面![]() ,因为
,因为![]() 面
面![]() ,所以
,所以![]() 平面
平面![]() .
.
(Ⅱ)同解法一.

【题目】为积极响应国家“阳光体育运动”的号召,某学校在了解到学生的实际运动情况后,发起以“走出教室,走到操场,走到阳光”为口号的课外活动倡议。为调查该校学生每周平均体育运动时间的情况,从高一高二基础年级与高三三个年级学生中按照4:3:3的比例分层抽样,收集300位学生每周平均体育运动时间的样本数据(单位:小时),得到如图所示的频率分布直方图。

(1)据图估计该校学生每周平均体育运动时间.并估计高一年级每周平均体育运动时间不足4小时的人数;
(2)规定每周平均体育运动时间不少于6小时记为“优秀”,否则为“非优秀”,在样本数据中,有30位高三学生的每周平均体育运动时间不少于6小时,请完成下列![]() 列联表,并判断是否有99%的把握认为“该校学生的每周平均体育运动时间是否“优秀”与年级有关”.
列联表,并判断是否有99%的把握认为“该校学生的每周平均体育运动时间是否“优秀”与年级有关”.
基础年级 | 高三 | 合计 | |
优秀 | |||
非优秀 | |||
合计 | 300 |
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附:K2![]() ,n=a+b+c+d.
,n=a+b+c+d.
【题目】每年春晚都是万众瞩目的时刻,这些节目体现的文化内涵、历史背景等反映了社会的进步.国家的富强,人民生活水平的提高等.某学校高三年级主任开学初为了解学生在看春晚后对节目体现的文化内涵、历史背景等是否会在今年的高考题中体现进行过思考,特地随机抽取100名高三学生(其中文科学生50,理科学生50名),进行了调查.统计数据如表所示(不完整):
“思考过” | “没有思考过” | 总计 | |
文科学生 | 40 | 10 | |
理科学生 | 30 | ||
总计 | 100 |
(1)补充完整所给表格,并根据表格数据计算是否有![]() 的把握认为看春晚后会思考节目体现的文化内涵、历史背景等与文理科学生有关;
的把握认为看春晚后会思考节目体现的文化内涵、历史背景等与文理科学生有关;
(2)①现从上表的”思考过”的文理科学生中按分层抽样选出7人.再从这7人中随机抽取4人,记这4人中“文科学生”的人数为![]() ,试求
,试求![]() 的分布列与数学期望;
的分布列与数学期望;
②现设计一份试卷(题目知识点来自春晚相关知识整合与变化),假设“思考过”的学生及格率为![]() ,“没有思考过”的学生的及格率为
,“没有思考过”的学生的及格率为![]() .现从“思考过”与“没有思考过”的学生中分别随机抽取一名学生进行测试,求两人至少有一个及格的概率.
.现从“思考过”与“没有思考过”的学生中分别随机抽取一名学生进行测试,求两人至少有一个及格的概率.
附参考公式: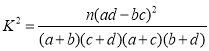 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 | 非优秀 | 总计 | |
甲班 | 10 | b | |
乙班 | c | 30 | |
总计105 |
已知在全部105人中随机抽取1人,成绩优秀的概率为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
参考公式: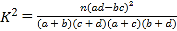
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
A.列联表中c的值为30,b的值为35
B.列联表中c的值为15,b的值为50
C.根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”
D.根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”