题目内容
已知二次函数f(x)=x2-ax+a(x∈R)同时满足:①不等式f(x)≤0的解集有且只有一个元素;②在定义域内存在0<x1<x2,使得不等式f(x1)>f(x2)成立.设数列{an}的前n项和Sn=f(n),(1)求数列{an}的通项公式;
(2)试构造一个数列{bn},(写出{bn}的一个通项公式)满足:对任意的正整数n都有bn<an,且
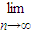
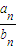 =2,并说明理由;
=2,并说明理由;(3)设各项均不为零的数列{cn}中,所有满足ci-ci+1<0的正整数i的个数称为这个数列{cn}的变号数.令cn=1-
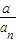 (n为正整数),求数列{cn}的变号数.
(n为正整数),求数列{cn}的变号数.
【答案】分析:(1)根据f(x)≤0的解集有且只有一个元素判断△等于0,求得a,则函数解析式可得,进而求得Sn.
(2)构造数列bn=n-k,任意的正整数n都有bn<an,则当n≥2时,n-k<2n-5恒成立,求得k的范围,进而根据bn≠0,k∉N*,求得bn.
(3)把(1)中求得的an代入cn=1- 中求得Cn,通过Cn+1-Cn>0判断数列{cn}递增,进而根据a4=-
中求得Cn,通过Cn+1-Cn>0判断数列{cn}递增,进而根据a4=- <0,1-
<0,1- >0n≥5,可知a4-a5<0,求得n≥3时,有且只有1个变号数;进而根据C1-C2<0,C2-C3<0,判断n≤2时变号数有2个,最后综合答案可得.
>0n≥5,可知a4-a5<0,求得n≥3时,有且只有1个变号数;进而根据C1-C2<0,C2-C3<0,判断n≤2时变号数有2个,最后综合答案可得.
解答:解:(1)∵f(x)≤0的解集有且只有一个元素,∴△=a2-4a=0
∴a=0或4,
当a=0时,函数f(x)=x2在(0,+∝)上递增,故不存在0<x1<x2,使得不等式f(x1)>f(x2)成立.
当a=4时,函数f(x)=x2-4x+4在(0,2)上递减,故存在0<x1<x2,使得不等式f(x1)>f(x2)成立.
an=Sn-Sn-1= 综上,得a=4,f(x)=x2-4x+4,∴Sn=n2-4n+4
综上,得a=4,f(x)=x2-4x+4,∴Sn=n2-4n+4
(2)要使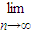
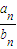 =2,,可构造数列bn=n-k,
=2,,可构造数列bn=n-k,
∵对任意的正整数n都有bn<an,
∴当n≥2时,n-k<2n-5恒成立,即n>5-k恒成立,即5-k<2
∴k>3,
又bn≠0,∴k∉N*,∴bn=n- ,.
,.
(3)由题设Cn=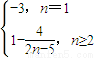 ,
,
∵n≥3时,Cn+1-Cn= -
-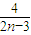 =
= >0,
>0,
∴n≥3时,数列{cn}递增,
∵a4=- <0,由1-
<0,由1-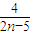 >0
>0
n≥5,可知a4-a5<0,即n≥3时,有且只有1个变号数;
又∵C1=-3,C2=-5,C3=-3,即C1-C2<0,C2-C3<0,∴此处变号数有2个.
综上得数列共有3个变号数,即变号数为3.
点评:本题主要考查了数列的递推式.递推式是数列中重要的内容,通过递推关系,观察,探求数列的规律,进而可求出整个数列的通项公式.通过递推关系的学习,可以培养学生的观察能力,归纳与转化能力,综合运用知识等能力,因此,是近几年高考与竞赛的热点.
(2)构造数列bn=n-k,任意的正整数n都有bn<an,则当n≥2时,n-k<2n-5恒成立,求得k的范围,进而根据bn≠0,k∉N*,求得bn.
(3)把(1)中求得的an代入cn=1-
 中求得Cn,通过Cn+1-Cn>0判断数列{cn}递增,进而根据a4=-
中求得Cn,通过Cn+1-Cn>0判断数列{cn}递增,进而根据a4=- <0,1-
<0,1- >0n≥5,可知a4-a5<0,求得n≥3时,有且只有1个变号数;进而根据C1-C2<0,C2-C3<0,判断n≤2时变号数有2个,最后综合答案可得.
>0n≥5,可知a4-a5<0,求得n≥3时,有且只有1个变号数;进而根据C1-C2<0,C2-C3<0,判断n≤2时变号数有2个,最后综合答案可得.解答:解:(1)∵f(x)≤0的解集有且只有一个元素,∴△=a2-4a=0
∴a=0或4,
当a=0时,函数f(x)=x2在(0,+∝)上递增,故不存在0<x1<x2,使得不等式f(x1)>f(x2)成立.
当a=4时,函数f(x)=x2-4x+4在(0,2)上递减,故存在0<x1<x2,使得不等式f(x1)>f(x2)成立.
an=Sn-Sn-1=
 综上,得a=4,f(x)=x2-4x+4,∴Sn=n2-4n+4
综上,得a=4,f(x)=x2-4x+4,∴Sn=n2-4n+4(2)要使
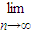
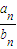 =2,,可构造数列bn=n-k,
=2,,可构造数列bn=n-k,∵对任意的正整数n都有bn<an,
∴当n≥2时,n-k<2n-5恒成立,即n>5-k恒成立,即5-k<2
∴k>3,
又bn≠0,∴k∉N*,∴bn=n-
 ,.
,.(3)由题设Cn=
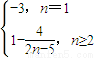 ,
,∵n≥3时,Cn+1-Cn=
 -
-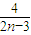 =
= >0,
>0,∴n≥3时,数列{cn}递增,
∵a4=-
 <0,由1-
<0,由1-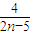 >0
>0n≥5,可知a4-a5<0,即n≥3时,有且只有1个变号数;
又∵C1=-3,C2=-5,C3=-3,即C1-C2<0,C2-C3<0,∴此处变号数有2个.
综上得数列共有3个变号数,即变号数为3.
点评:本题主要考查了数列的递推式.递推式是数列中重要的内容,通过递推关系,观察,探求数列的规律,进而可求出整个数列的通项公式.通过递推关系的学习,可以培养学生的观察能力,归纳与转化能力,综合运用知识等能力,因此,是近几年高考与竞赛的热点.

练习册系列答案
相关题目