题目内容
【题目】已知抛物线![]() :
:![]() 和直线
和直线![]() :
:![]() ,
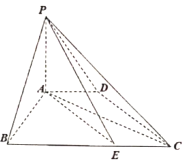
,![]() 是直线上
是直线上![]() 一点,过点
一点,过点![]() 做抛物线的两条切线,切点分别为
做抛物线的两条切线,切点分别为![]() ,
,![]() ,
,![]() 是抛物线上异于
是抛物线上异于![]() ,
,![]() 的任一点,抛物线在
的任一点,抛物线在![]() 处的切线与
处的切线与![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() ,则
,则![]() 外接圆面积的最小值为______.
外接圆面积的最小值为______.
【答案】![]()
【解析】
设三个切点分别为![]() ,求出三条切线
,求出三条切线![]() 方程,三条切线方程分别联立求出
方程,三条切线方程分别联立求出![]() 坐标,点
坐标,点![]() 在直线
在直线![]() 上,得到
上,得到![]() 关系,求出
关系,求出![]() ,进而求出
,进而求出![]() ,设三角形
,设三角形![]() 外接圆半径为
外接圆半径为![]() ,利用
,利用![]() ,求出
,求出![]() 的解析式,根据其特征,求出最小值.
的解析式,根据其特征,求出最小值.
设三个切点分别为![]() ,
,
若在点![]() 处的切线斜率存在,
处的切线斜率存在,
设方程为![]() 与
与![]() 联立,
联立,
得,![]() ,
,
即![]() ,
,
所以切线![]() 方程为
方程为![]() ①
①
若在点![]() 的切线斜率不存在,则
的切线斜率不存在,则![]() ,
,
切线方程为![]() 满足①方程,
满足①方程,
同理切线![]() 的方程分别为
的方程分别为![]() ,
,
![]() ,联立
,联立![]() 方程,
方程,
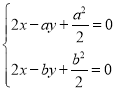 ,解得
,解得 ,即
,即![]()
同理![]() ,
,![]() ,
,
![]() ,
,
设![]() 外接圆半径为
外接圆半径为![]() ,
,
![]() ,
,
![]()
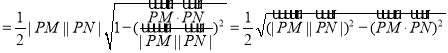
![]()
![]() ,
,
![]()
![]() 时取等号,
时取等号,
点![]() 在直线
在直线![]() ,
,
![]()
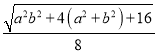
![]()
![]() ,
,
当且仅当![]() 或
或![]() 时等号成立,
时等号成立,
此时![]() 外接圆面积最小为
外接圆面积最小为![]() .
.
故答案为:![]() .
.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目