题目内容
已知椭圆的中心在原点,焦点在x轴上,离心率为 ,且经过点
,且经过点 ,直线
,直线 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B.
(Ⅰ)求椭圆的方程;
(Ⅱ)求m的取值范围;
(Ⅲ)若直线 不过点M,求证:直线MA、MB与x轴围成一个等腰三角形
不过点M,求证:直线MA、MB与x轴围成一个等腰三角形
 ,且经过点
,且经过点 ,直线
,直线 交椭圆于不同的两点A,B.
交椭圆于不同的两点A,B.(Ⅰ)求椭圆的方程;
(Ⅱ)求m的取值范围;
(Ⅲ)若直线
 不过点M,求证:直线MA、MB与x轴围成一个等腰三角形
不过点M,求证:直线MA、MB与x轴围成一个等腰三角形(Ⅰ)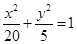 ;(Ⅱ)
;(Ⅱ)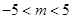 ;(Ⅲ)参考解析
;(Ⅲ)参考解析
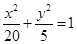 ;(Ⅱ)
;(Ⅱ)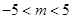 ;(Ⅲ)参考解析
;(Ⅲ)参考解析试题分析:(Ⅰ)已知椭圆的焦点在x轴上,离心率为
 ,且经过点
,且经过点 ,利用待定系数法求出椭圆的方程.
,利用待定系数法求出椭圆的方程.(Ⅱ)由于直线
 交椭圆于不同的两点A,B.所以直线与椭圆方程联立消去y后,得到关于x的一元二次方程,这个方程的的判别式要大于零即可求出m的范围.
交椭圆于不同的两点A,B.所以直线与椭圆方程联立消去y后,得到关于x的一元二次方程,这个方程的的判别式要大于零即可求出m的范围.(Ⅲ)直线
 不过点M,要求证直线MA、MB与x轴围成一个等腰三角形.将该问题等价转化为直线MA与直线MB的斜率何为零.所以通过计算两直线的斜率,并用A,B的坐标表示,通过通分整理再结合(Ⅱ)所得的韦达定理即可得分子为零.及证明了斜率和为零从而可结论.
不过点M,要求证直线MA、MB与x轴围成一个等腰三角形.将该问题等价转化为直线MA与直线MB的斜率何为零.所以通过计算两直线的斜率,并用A,B的坐标表示,通过通分整理再结合(Ⅱ)所得的韦达定理即可得分子为零.及证明了斜率和为零从而可结论.试题解析:(Ⅰ)设椭圆的方程为
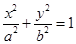 ,因为
,因为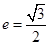 ,所以
,所以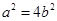 ,又因为
,又因为 ,所以
,所以 ,解得
,解得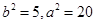 ,故椭圆方程为
,故椭圆方程为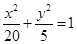
(Ⅱ)将
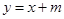 代入
代入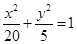 并整理得
并整理得 ,
,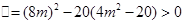 ,解得
,解得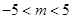
(Ⅲ)设直线
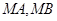 的斜率分别为
的斜率分别为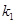 和
和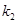 ,只要证明
,只要证明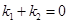 .设
.设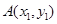 ,
,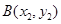 ,
,则
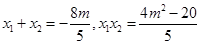 。
。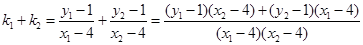
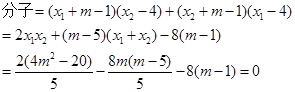

练习册系列答案
相关题目
 ,
, ,动点G满足
,动点G满足 .
. 的方程;
的方程; 且与
且与 轴不垂直的直线l交(Ⅰ)中的轨迹
轴不垂直的直线l交(Ⅰ)中的轨迹 上是否存在点
上是否存在点 ,使得以MP,MQ为邻边的平行四边形是菱形?若存在,求实数m的取值范围;若不存在,请说明理由.
,使得以MP,MQ为邻边的平行四边形是菱形?若存在,求实数m的取值范围;若不存在,请说明理由. 的直线与曲线M相交于A、B两点. 问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由.
的直线与曲线M相交于A、B两点. 问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由.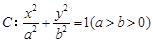 的离心率为
的离心率为 ,其中左焦点
,其中左焦点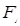 (-2,0).
(-2,0).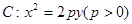 的焦点为
的焦点为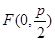 ,准线为
,准线为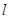 ,点
,点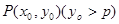 为抛物线C上的一点,且
为抛物线C上的一点,且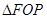 的外接圆圆心到准线的距离为
的外接圆圆心到准线的距离为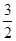 .
.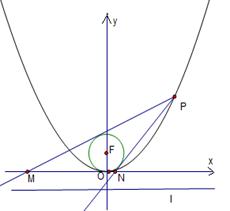
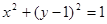 ,过点P作圆F的2条切线分别交
,过点P作圆F的2条切线分别交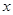 轴于点
轴于点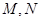 ,求
,求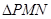 面积的最小值时
面积的最小值时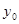 的值.
的值. 为椭圆
为椭圆 上任意一点,
上任意一点, 、
、 为左右焦点.如图所示:
为左右焦点.如图所示: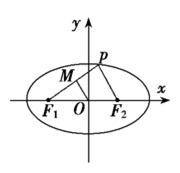
 的中点为
的中点为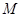 ,求证
,求证 ;
; ,求
,求 的值.
的值.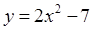 ,求曲线过点
,求曲线过点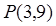 的切线方程。
的切线方程。 的圆心为抛物线
的圆心为抛物线 的焦点,直线
的焦点,直线 与圆
与圆 相切,则该圆的方程为( )
相切,则该圆的方程为( )



 ,椭圆E的内接平行四边形的一组对边分别经过它的两个焦点(如图),则这个平行四边形面积的最大值是 .
,椭圆E的内接平行四边形的一组对边分别经过它的两个焦点(如图),则这个平行四边形面积的最大值是 .