题目内容
给定椭圆C: ,若椭圆C的一个焦点为F(
,若椭圆C的一个焦点为F( ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为 .
.
(I)求椭圆C的方程;
(II)已知斜率为k(k≠0)的直线l与椭圆C交于不同的两点A,B,点Q满足 且
且 =0,其中N为椭圆的下顶点,求直线在y轴上截距的取值范围.
=0,其中N为椭圆的下顶点,求直线在y轴上截距的取值范围.
 ,若椭圆C的一个焦点为F(
,若椭圆C的一个焦点为F( ,0),其短轴上的一个端点到F的距离为
,0),其短轴上的一个端点到F的距离为 .
.(I)求椭圆C的方程;
(II)已知斜率为k(k≠0)的直线l与椭圆C交于不同的两点A,B,点Q满足
 且
且 =0,其中N为椭圆的下顶点,求直线在y轴上截距的取值范围.
=0,其中N为椭圆的下顶点,求直线在y轴上截距的取值范围.(I) .(II)
.(II) .(III)直线
.(III)直线 纵截距的范围是
纵截距的范围是 .
.
 .(II)
.(II) .(III)直线
.(III)直线 纵截距的范围是
纵截距的范围是 .
.试题分析:(I)由题意联立方程组
由
 得
得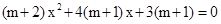 ,
,根据
 ,即可得到
,即可得到 的取值范围是
的取值范围是 .
.(II)设直线方程为
 ,
,通过联立
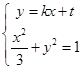
设
 应用韦达定理,结合
应用韦达定理,结合 得
得 为
为 的中点,
的中点, ,
,得到
 ,可建立
,可建立 的方程, 从而由
的方程, 从而由 得到
得到 使问题得解.
使问题得解.试题解析:(I)由题意知
 .
.由
 得
得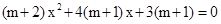 ,
,所以
 ,解得
,解得 ,
,所以求
 的取值范围是
的取值范围是 .
.(II)设直线方程为
 ,
,由
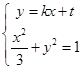 整理得
整理得 ,
,化简得

设

则

由
 得
得 为
为 的中点,所以
的中点,所以
因为
 ,所以
,所以
即
 ,化简得
,化简得
又
 ,
,所以

又
 ,所以
,所以
 .
.
练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
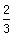 ,且过点
,且过点 ,点A、B分别是椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
,点A、B分别是椭圆C长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于 轴上方,
轴上方, .
.
 的最小值.
的最小值. ,直线AM、BM相交于点M,且这两条直线的斜率之积为
,直线AM、BM相交于点M,且这两条直线的斜率之积为 .
. (
( )相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R.
)相切于点E、F,又PE、PF与曲线C的另一交点分别为Q、R. ,椭圆
,椭圆 以
以 的长轴为短轴,且与
的长轴为短轴,且与 ,求直线
,求直线 的方程.
的方程. ,
, ,动点G满足
,动点G满足 .
. 的方程;
的方程; 且与
且与 轴不垂直的直线l交(Ⅰ)中的轨迹
轴不垂直的直线l交(Ⅰ)中的轨迹 上是否存在点
上是否存在点 ,使得以MP,MQ为邻边的平行四边形是菱形?若存在,求实数m的取值范围;若不存在,请说明理由.
,使得以MP,MQ为邻边的平行四边形是菱形?若存在,求实数m的取值范围;若不存在,请说明理由. 的直线与曲线M相交于A、B两点. 问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由.
的直线与曲线M相交于A、B两点. 问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由. 的圆心为抛物线
的圆心为抛物线 的焦点,直线
的焦点,直线 与圆
与圆 相切,则该圆的方程为( )
相切,则该圆的方程为( )



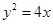 焦点
焦点 的直线
的直线 与抛物线相交于
与抛物线相交于 两点,若
两点,若 ,则
,则 .
. ,椭圆E的内接平行四边形的一组对边分别经过它的两个焦点(如图),则这个平行四边形面积的最大值是 .
,椭圆E的内接平行四边形的一组对边分别经过它的两个焦点(如图),则这个平行四边形面积的最大值是 .