题目内容
平面内有两个定点F1,F2和一动点M,设命题甲,||MF1|-|MF2||是定值,命题乙:点M的轨迹是双曲线,则命题甲是命题乙的( )A.充分但不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】分析:先根据||MF1|-|MF2||是定值可得到动点M的轨迹即是双曲线,即命题乙正确;再由点M的轨迹是双曲线可得到动点M到两定点的距离的差的绝对值等于定值,即命题甲正确,从而可得到答案.
解答:解:命题甲:||MF1|-|MF2||是定值可得到动点M的轨迹不一定是双曲线,可推不出命题乙,故不充分
命题乙:点M的轨迹是双曲线,则可得到M到两定点的距离的差的绝对值等于一常数,即可推出命题甲,故必要
∴命题甲是命题乙的必要不充分条件.
故选B.
点评:本题主要考查双曲线的定义和充分、必要条件的判定.考查知识的综合运用能力.
解答:解:命题甲:||MF1|-|MF2||是定值可得到动点M的轨迹不一定是双曲线,可推不出命题乙,故不充分
命题乙:点M的轨迹是双曲线,则可得到M到两定点的距离的差的绝对值等于一常数,即可推出命题甲,故必要
∴命题甲是命题乙的必要不充分条件.
故选B.
点评:本题主要考查双曲线的定义和充分、必要条件的判定.考查知识的综合运用能力.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
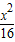 -
- =1(x≤-4)
=1(x≤-4) -
- =1(x≤-3)
=1(x≤-3) -
- =1(x>≥4)
=1(x>≥4) -
- =1(x≥3)
=1(x≥3)