题目内容
已知直线AB上的两点A(-2,1),B(
,4+2
),直线l的斜率为kl,倾斜角为θ.
(1)若l⊥AB,求角θ的值;
(2)若直线l过点P(-1,
),且A,B两点到直线l的距离相等,求kl的值.
| 3 |
| 3 |
(1)若l⊥AB,求角θ的值;
(2)若直线l过点P(-1,
| 5 |
| 2 |
(1)∵两点A(-2,1),B(
,4+2
),由斜率公式可得
直线AB的斜率kAB=
=
=
,
又因为l⊥AB,所以kl•kAB=-1,代入解得kl=-
,
即tanθ=-
,又0°≤θ<180°,∴θ=150°
(2)所求直线l满足A,B两点到直线l的距离相等,
必有l∥AB或l过AB的中点,
当l∥AB时,kl=kAB=
,
当直线l过AB的中点(
,
)时,
kl=kAP=
=
=
=3-
,
故kl的值为:
或3-
| 3 |
| 3 |
直线AB的斜率kAB=
4+2
| ||
|
(3+2
| ||||
(2+
|
| 3 |
又因为l⊥AB,所以kl•kAB=-1,代入解得kl=-
| ||
| 3 |
即tanθ=-
| ||
| 3 |
(2)所求直线l满足A,B两点到直线l的距离相等,
必有l∥AB或l过AB的中点,
当l∥AB时,kl=kAB=
| 3 |
当直线l过AB的中点(
| ||
| 2 |
5+2
| ||
| 2 |
kl=kAP=
| ||||||
|
2
| ||
|
2
| ||||
(
|
| 3 |
故kl的值为:
| 3 |
| 3 |

练习册系列答案
相关题目
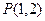 的直线,且使
的直线,且使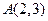 ,
,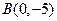 到它的距离相等的直线方程。
到它的距离相等的直线方程。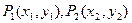 分别是直线
分别是直线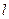 上和直线
上和直线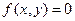 ,则方程
,则方程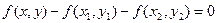 表示
表示