题目内容
【题目】设数列{an}的前n项和为Sn ， 已知2Sn=3n+1+2n﹣3．
（1）求数列{an}的通项公式；
（2）求数列{nan}的前n项和Tn ．
【答案】
（1）解：∵2Sn=3n+1+2n﹣3，
∴当n≥2时，2an=2Sn﹣2Sn﹣1=（3n+1+2n﹣3）﹣[3n+2（n﹣1）﹣3]=23n+2，
∴an=3n+1，
又a1=S1= 
（32+2×1﹣3）=4，适合上式，
∴an=3n+1；
（2）解：由（1）知an=3n+1，则nan=n3n+n，
∵数列{nan}的前n项和Tn，
则Tn=131+232+…+n3n+（1+2+3+…+n），
令An=131+232+…+n3n，①
则3An=132+233+…+（n﹣1）3n+n3n+1，②
①﹣②得：﹣2An=31+32+…+3n﹣n3n+1
= 
﹣n3n+1=（ 
）3n+1﹣ 
，
∴An= 
3n+1+ 
．
∴Tn= 3n+1+ 
+
【解析】（1）由Sn=3n+1+2n﹣3，可得当n≥2时，an=Sn﹣Sn﹣1=3n+1，再检验当n=1时，a1是否适合上式，即可求得数列{an}的通项公式；（2）依题意，nan=n3n+n，Tn=131+232+…+n3n+（1+2+3+…+n），令An=131+232+…+n3n ， 利用错位相减法可求得An= 3n+1+ ，而1+2+3+…+n= ，从而可得数列{nan}的前n项和Tn ．
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系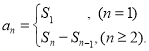
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．
天天向上口算本系列答案
【题目】在用“五点法”画函数f（x）=Asin（ωx+φ）（ω＞0，|φ|＜ 
）在某一周期内的图象时，列表并填入了部分数据，如下表：
ωx+φ | 0 |
| π |
| 2π |
x | π |
| |||
Asin（ωx+φ） | 0 | 3 | ﹣3 | 0 |
（1）请将上表空格中处所缺的数据填写在答题卡的相应位置上，并直接写出函数f（x）的解析式；
（2）将y=f（x）图象上所有点的横坐标缩短为原来的 
，再将所得图象向左平移 
个单位，得到y=g（x）的图象，求g（x）的单调递增区间．
