题目内容
【题目】给出下列命题:
①已知向量![]() 与
与![]() 的夹角是钝角,则实数
的夹角是钝角,则实数![]() 的取值范围是
的取值范围是![]() ;
;
②函数![]() 与
与![]() 的图像关于
的图像关于![]() 对称;
对称;
③函数![]() 的最小正周期为
的最小正周期为![]() ;
;
④函数 为周期函数;
为周期函数;
⑤函数![]() 的图像关于点
的图像关于点![]() 对称的函数图像的解析式为
对称的函数图像的解析式为![]()
其中正确命题的序号为__________.
【答案】③④⑤
【解析】
依次判断每个选项的正误,①举出向量平行时的反例得出错误,②举例函数![]() 得出错误,③画出图像得到周期,④找到1为函数的周期,⑤设对称函数上一点
得出错误,③画出图像得到周期,④找到1为函数的周期,⑤设对称函数上一点![]() ,则关于
,则关于![]() 对称的点为
对称的点为![]() 在
在![]() 上,得到答案.
上,得到答案.
①已知向量,![]() 与
与![]() 的夹角是钝角,则实数
的夹角是钝角,则实数![]() 的取值范围是
的取值范围是![]()
当![]() 时两向量平行,不满足夹角为钝角,错误
时两向量平行,不满足夹角为钝角,错误
②函数![]() 与
与![]() 的图像关于
的图像关于![]() 对称;
对称;
取![]() 则
则![]() 和
和![]() 不关于
不关于![]() 对称,错误.
对称,错误.
③函数![]() 的最小正周期为
的最小正周期为![]() ;
;
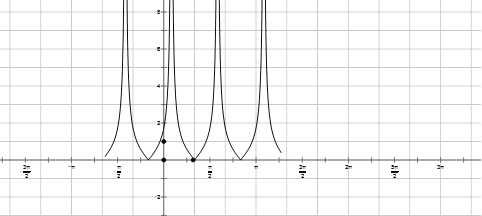
画出图像知,命题正确
④函数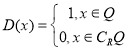 为周期函数
为周期函数
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
故 ,故为周期函数,正确
,故为周期函数,正确
⑤函数![]() 的图像关于点
的图像关于点![]() 对称的函数图像的解析式为
对称的函数图像的解析式为![]()
设对称函数上一点![]() ,则关于
,则关于![]() 对称的点为
对称的点为![]() 在
在![]() 上
上
即![]() ,正确
,正确
故答案为③④⑤

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案【题目】为了解某高校学生中午午休时间玩手机情况,随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图,将日均午休时玩手机不低于40分钟的学生称为“手机控”.

(1)求列联表中未知量的值;
非手机控 | 手机控 | 合计 | |
男 |
|
|
|
女 |
| 10 | 55 |
合计 |
(2)能否有![]() 的把握认为“手机控与性别有关”?
的把握认为“手机控与性别有关”?
 .
.
| 0.05 | 0.10 |
| 3.841 | 6.635 |
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有![]() 的把握认为“微信控”与“性别”有关?
的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,再随机抽取3人赠送礼品,试求抽取3人中恰有2人是“微信控”的概率.
参考公式: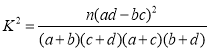 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.040 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |