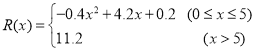题目内容
【题目】已知函数![]()
(Ⅰ)若![]() 的定义域和值域均是
的定义域和值域均是![]() ,求实数
,求实数![]() 的值;
的值;
(Ⅱ)若![]() 在区间
在区间![]() 上是减函数,且对任意的
上是减函数,且对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)若![]() ,且对任意的
,且对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)2(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
试题分析:(I)由函数f(x)的解析式,可得函数在(-∞,a]上单调递减,进而得到f(x)在[1,a]上单调递减,则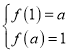 ,由此构造关于a的方程组,解之可得答案.(Ⅱ)若f(x)在区间(-∞,2]上是减函数,则(-∞,2](-∞,a],进而结合x∈[1,a+1]时,f(x)max=f(1),构造关于a的不等式,解不等式,可得答案.(III)由函数g(x)在[0,1]上递增,f(x)在[0,1]上递减,可分别求出两个函数的值域,若对任意的x∈[0,1],都存在x0∈[0,1],使得f(x0)=g(x)成立;则两个函数的值域满足:[1,3][6-2a,5],进而可得答案
,由此构造关于a的方程组,解之可得答案.(Ⅱ)若f(x)在区间(-∞,2]上是减函数,则(-∞,2](-∞,a],进而结合x∈[1,a+1]时,f(x)max=f(1),构造关于a的不等式,解不等式,可得答案.(III)由函数g(x)在[0,1]上递增,f(x)在[0,1]上递减,可分别求出两个函数的值域,若对任意的x∈[0,1],都存在x0∈[0,1],使得f(x0)=g(x)成立;则两个函数的值域满足:[1,3][6-2a,5],进而可得答案
试题解析:(Ⅰ)∵![]()
∴![]() 在
在![]() 上单调递减,又
上单调递减,又![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() , ∴
, ∴![]() , ∴
, ∴![]()
(Ⅱ)∵![]() 在区间
在区间![]() 上是减函数, ∴
上是减函数, ∴![]() ∴
∴![]()
∴![]() ,
,![]()
∴![]() 时,
时,![]()
又∵对任意的![]() ,都有
,都有![]() ,
,
∴![]() , 即
, 即 ![]() , ∴
, ∴![]()
(Ⅲ)∵![]() 在
在![]() 上递增,
上递增,![]() 在
在![]() 上递减,
上递减,
当![]() 时,
时,![]() ,
,![]()
∵对任意的![]() ,都存在
,都存在![]() ,使得
,使得![]() 成立;
成立;
∴![]()
![]()
∴![]()
![]()

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
【题目】某车间将10名技工平均分为甲,乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
1号 | 2号 | 3号 | 4号 | 5号 | |
甲组 | 4 | 5 | 7 | 9 | 10 |
乙组 | 5 | 6 | 7 | 8 | 9 |
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此判断哪组工人的技术水平更好;
(2)质监部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,否则“不合格”.求该车间“质量不合格”的概率.