Question

【题目】如图，AB是⊙O的直径，C、F是⊙O上的两点，OC⊥AB，过点F作⊙O的切线FD交AB的延长线于点D．连接CF交AB于点E．

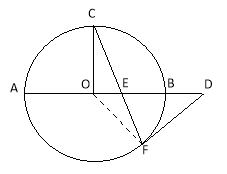
（1）求证：DE2=DBDA；

（2）若DB=2，DF=4，试求CE的长．

Answer 1

【答案】（1）证明见解析；（2）

【解析】

试题分析：（1）由切割线定理有，因此只要证明，也即只要证明，再考虑它们的余角是否相等即得；（2）由（1）可得的长，从而有圆的半径，再得，最后由勾股定理可得．

试题解析：（1）证明：连接OF．

因为DF切⊙O于F，所以∠OFD=90°．

所以∠OFC+∠CFD=90°．

因为CO⊥AB于O，所以∠OCF+∠CEO=90°．

所以∠CFD=∠CEO=∠DEF，所以DF=DE．

因为DF是⊙O的切线，所以DF2=DBDA．

所以DE2=DBDA．

（2）解：DF2=DBDA，DB=2，DF=4．

DA=8，从而AB=6，则．

又由（1）可知，DE=DF=4，BE=2，OE=1．

从而在中，．