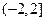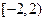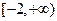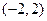题目内容
设A={x|–2≤x≤a},B={y|y=2x+3,且x∈A},C={z|z=x2,且x∈A },若C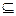 B,求实数a的取值范围.
B,求实数a的取值范围.
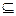 B,求实数a的取值范围.
B,求实数a的取值范围.a的取值范围是(–∞,–2)∪[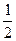 ,3]
,3]
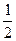 ,3]
,3]∵y=2x+3在[–2, a]上是增函数
∴–1≤y≤2a+3,即B={y|–1≤y≤2a+3}
作出z=x2的图像,该函数定义域右端点x=a有三种不同的位置情况如下: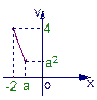
①当–2≤a≤0时,a2≤z≤4即C={z|a2≤z≤4}
要使C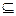 B,必须且只须2a+3≥4得a≥
B,必须且只须2a+3≥4得a≥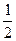 与–2≤a<0矛盾
与–2≤a<0矛盾
②当0≤a≤2时,0≤z≤4即C={z|0≤z≤4},要使C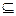 B,由图可知:
B,由图可知:
必须且只需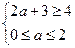
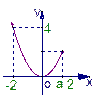
解得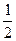 ≤a≤2
≤a≤2
③当a>2时,0≤z≤a2,即C={z|0≤z≤a2},
要使C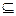 B必须且只需
B必须且只需
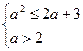 解得2<a≤3
解得2<a≤3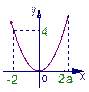
④当a<–2时,A=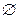 此时B=C=
此时B=C=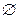 ,则C
,则C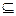 B成立.
B成立.
综上所述,a的取值范围是(–∞,–2)∪[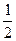 ,3].
,3].
∴–1≤y≤2a+3,即B={y|–1≤y≤2a+3}
作出z=x2的图像,该函数定义域右端点x=a有三种不同的位置情况如下:

①当–2≤a≤0时,a2≤z≤4即C={z|a2≤z≤4}
要使C
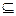 B,必须且只须2a+3≥4得a≥
B,必须且只须2a+3≥4得a≥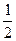 与–2≤a<0矛盾
与–2≤a<0矛盾
②当0≤a≤2时,0≤z≤4即C={z|0≤z≤4},要使C
 B,由图可知:
B,由图可知: 必须且只需
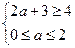
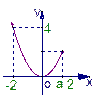
解得
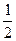 ≤a≤2
≤a≤2③当a>2时,0≤z≤a2,即C={z|0≤z≤a2},
要使C
 B必须且只需
B必须且只需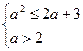 解得2<a≤3
解得2<a≤3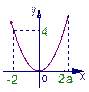
④当a<–2时,A=
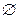 此时B=C=
此时B=C= ,则C
,则C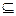 B成立.
B成立. 综上所述,a的取值范围是(–∞,–2)∪[
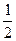 ,3].
,3]. 
练习册系列答案
相关题目
 A,且A∩B={1,a}?若存在,求出实数a的值;若不存在,说明理由.
A,且A∩B={1,a}?若存在,求出实数a的值;若不存在,说明理由. ,
,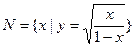 ,则
,则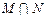 =
=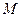
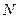
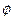
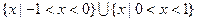
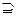 B且B≠
B且B≠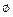 ,求实数m的取值范围。
,求实数m的取值范围。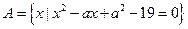 ,
,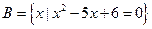 ,
,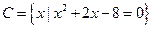 满足
满足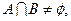 ,
,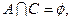 求实数
求实数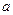 的值。
的值。
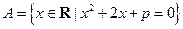 ,且
,且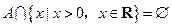 ,
,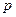 的取值范围.
的取值范围.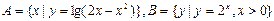 ,R是实数集,则
,R是实数集,则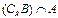 =( )
=( )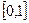
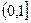
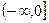
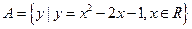 ,
,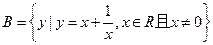 ,则
,则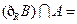 ()
()