题目内容
已知集合A={a,a+b,a+2b},B={a,ac,ac2}.若A=B,求c的值.

分两种情况进行讨论. 
(1)若a+b=ac且a+2b=ac2,消去b得:a+ac2-2ac=0,
a=0时,集合B中的三元素均为零,和元素的互异性相矛盾,故a≠0.
∴c2-2c+1=0,即c=1,但c=1时,B中的三元素又相同,此时无解.
(2)若a+b=ac2且a+2b=ac,消去b得:2ac2-ac-a=0,
∵a≠0,∴2c2-c-1=0,即(c-1)(2c+1)=0,又c≠1,故c=-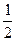


(1)若a+b=ac且a+2b=ac2,消去b得:a+ac2-2ac=0,

a=0时,集合B中的三元素均为零,和元素的互异性相矛盾,故a≠0.

∴c2-2c+1=0,即c=1,但c=1时,B中的三元素又相同,此时无解.

(2)若a+b=ac2且a+2b=ac,消去b得:2ac2-ac-a=0,

∵a≠0,∴2c2-c-1=0,即(c-1)(2c+1)=0,又c≠1,故c=-
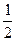

要解决c的求值问题,关键是要有方程的数学思想,此题应根据相等的两个集合元素完全相同及集合中元素的确定性、互异性,无序性建立关系式.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
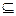 B,求实数a的取值范围.
B,求实数a的取值范围. ,集合
,集合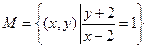 ,
,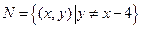 ,那么
,那么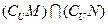 等于________________。
等于________________。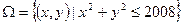 ,若点
,若点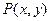 、点
、点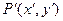 满足
满足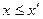 且
且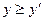 ,则称点
,则称点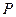 优于
优于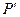 . 如果集合
. 如果集合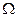 中的点
中的点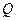 满足:不存在
满足:不存在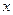 的不等式
的不等式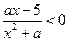 的解集为
的解集为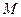 ,
,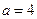 时,求解集
时,求解集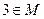 ,且
,且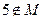 ,求实数
,求实数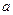 的取值范围。
的取值范围。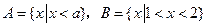 ,且
,且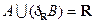 ,则实数
,则实数 的取值范围
的取值范围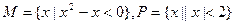 ,则
,则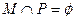
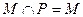
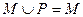
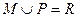
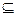 {a1, a2, a3, a4},且M∩{a1 ,a2, a3}="{" a1,a2}的集合M的个数是( )
{a1, a2, a3, a4},且M∩{a1 ,a2, a3}="{" a1,a2}的集合M的个数是( )