题目内容
6.函数$y=\frac{1}{x+1}$的单调递减区间为(-∞,-1)和(-1,+∞).分析 根据分式函数的性质进行求解即可.
解答 解:将函数y=$\frac{1}{x}$的图象向左平移一个单位得到$y=\frac{1}{x+1}$,
∵y=$\frac{1}{x}$的单调递减区间为(-∞,0)和(0,+∞),
∴$y=\frac{1}{x+1}$的单调递减区间为(-∞,-1)和(-1,+∞),
故答案为:(-∞,-1)和(-1,+∞).
点评 本题主要考查函数单调递减区间的求解,根据分式函数的性质是解决本题的关键.

练习册系列答案
相关题目
16.不等式(x+5)(3-2x)≥6的解集是( )
| A. | {x|-$\frac{9}{2}$≤x≤1} | B. | {x|-1≤x≤$\frac{9}{2}$} | C. | {x|x≤-$\frac{9}{2}$或x≥1} | D. | {x|x≤-1或x≥$\frac{9}{2}$} |
17.若$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是同一个平面α内的两个向量,则( )
| A. | 平面α内任一向量$\overrightarrow{a}$,都有$\overrightarrow{a}$=λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$(λ,μ∈R) | |
| B. | 若存在实数λ1,λ2,使λ1$\overrightarrow{{e}_{1}}$+λ2$\overrightarrow{{e}_{2}}$=0,则λ1=λ2=0 | |
| C. | 若$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$不共线,则空间任一向量$\overrightarrow{a}$,都有$\overrightarrow{a}$=λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$(λ,μ∈R) | |
| D. | 若$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$不共线,则平面任一向量$\overrightarrow{a}$,都有$\overrightarrow{a}$=λ$\overrightarrow{{e}_{1}}$+μ$\overrightarrow{{e}_{2}}$(λ,μ∈R) |
18.若将函数f(x)=2sin(3x+$\frac{5π}{12}$)的图象向右平移$\frac{2π}{9}$个单位后得到函数g(x)的图象,g($\frac{1}{3}$x)在[-$\frac{π}{3}$,$\frac{5π}{6}$]上的最大值( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 2 |
15.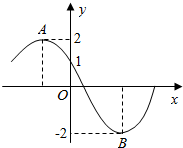 如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )
如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )
 如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )
如图为函数f(x)=Msin(ωx+φ)(M>0,ω>0,0≤φ≤π)的部分图象,若点A、B分别为函数f(x)的最高点与最低点,且|AB|=5,那么f(-1)=( )| A. | 2 | B. | $\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | -2 |
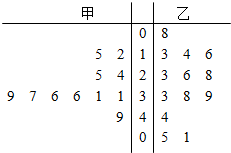 某赛季甲,乙两名篮球运动员每场比赛得分可用茎叶图表示如下:
某赛季甲,乙两名篮球运动员每场比赛得分可用茎叶图表示如下: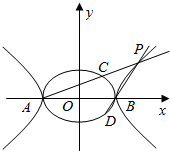 如图,椭圆C1:x2+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左、右顶点分别为A,B,点P为双曲线C2:x2-$\frac{{y}^{2}}{{b}^{2}}$=1在第一象限内的图象上一点,直线AP,BP与椭圆C1分别交于C,D两点.C是AP的中点.
如图,椭圆C1:x2+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左、右顶点分别为A,B,点P为双曲线C2:x2-$\frac{{y}^{2}}{{b}^{2}}$=1在第一象限内的图象上一点,直线AP,BP与椭圆C1分别交于C,D两点.C是AP的中点.