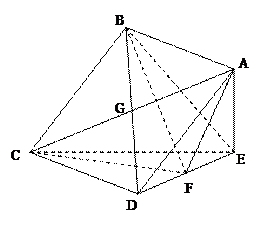题目内容
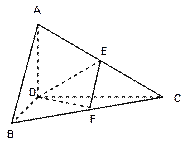
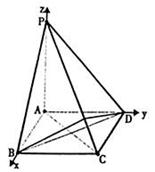
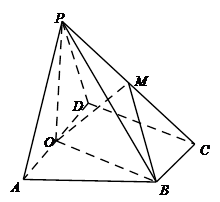
如图,在四棱锥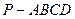 中,底面
中,底面 是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
是矩形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.
证明:(1)连结AC交BD于O,连结EO。
∵底面ABCD是正方形,
∴点O是AC的中点。
又∵E是PC的中点
∴在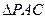 中,EO为中位线
中,EO为中位线
∴PA∥EO。 …………………….3分
而EO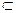 平面EDB,PA
平面EDB,PA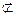 平面EDB,
平面EDB,
∴PA∥平面EDB。 ……………………6分
(2)由PD⊥底面ABCD,得PD⊥BC。
∵底面ABCD是正方形,
∴DC⊥BC,
∴BC⊥平面PDC,而DE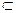 平面PDC,
平面PDC,
∴BC⊥DE。① ……………………8分 PD=DC,E是PC的中点,
PD=DC,E是PC的中点,
∴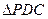 是等腰三角形,DE⊥PC。② ……………………10分
是等腰三角形,DE⊥PC。② ……………………10分
由①和②得DE⊥平面PBC。
而PB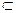 平面PBC,
平面PBC,
∴DE⊥PB。 ……………………12分
又EF⊥PB且DE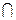 EF=E,
EF=E,
∴PB⊥平面EFD。
解析

练习册系列答案
相关题目
[2014·宁化模拟]若向量a=(2x,1,3),b=(1,-2y,9),且a∥b,则( )
| A.x=1,y=1 | B.x=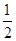 ,y=- ,y=-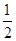 |
C.x= ,y=- ,y=-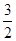 | D.x=- ,y= ,y=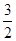 |
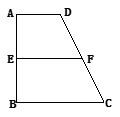
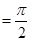 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE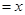 ,G是BC的中点.沿EF将梯形ABCD翻折,
,G是BC的中点.沿EF将梯形ABCD翻折,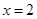 时,求证:BD⊥EG ;
时,求证:BD⊥EG ;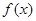 ,求
,求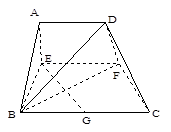
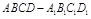 的底面
的底面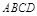 是菱形,
是菱形,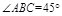 ,其侧面展开图是边长为
,其侧面展开图是边长为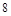 的正方形.
的正方形.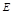 、
、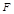 分别是侧棱
分别是侧棱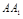 、
、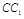 上的动点,
上的动点,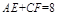 .
.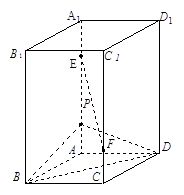
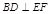 ;
;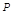 在棱
在棱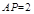 ,若
,若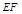 ∥平面
∥平面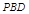 ,求
,求 .
.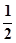 AD=1,CD=
AD=1,CD=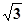 .
.
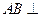 平面
平面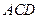 ,
,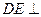 平面
平面 ,△
,△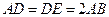 ,
,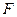 为
为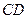 的中点.
的中点.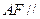 平面
平面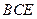 ;
;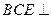 平面
平面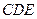 ;
;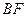 和平面
和平面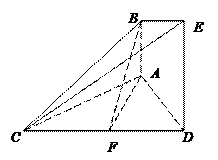
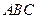 的边长为4,
的边长为4,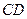 是
是 边上的高,
边上的高,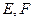 分别是
分别是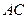 和
和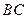 边的中点,现将△
边的中点,现将△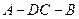 .
.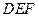 的位置关系,并说明理由;
的位置关系,并说明理由;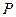 ,使
,使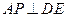 ?证明你的结论.
?证明你的结论.