题目内容
设函数y=xsinx+cosx的图象上的点（x0，y0）的切线的斜率为k，若k=g（x0），则函数k=g（x0），x0∈[-π，π]的图象大致为（ ）
A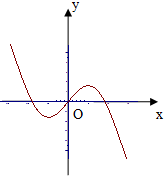． | B． |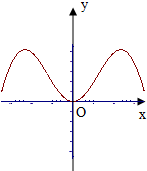
C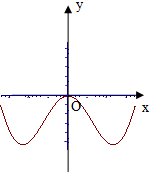． | D． |
由题意，得g（x）=xcosx，因为g（-x）=-g（x）所以它是奇函数．
k=g（x0）=y′（x0）=x0cosx0，
注意到g（x）为奇函数，故其图象关于原点中心对称．排除B，C．
又当0＜x＜1＜
时，cosx＞0，∴xcosx＞0，知D项不符合，
故选A．
k=g（x0）=y′（x0）=x0cosx0，
注意到g（x）为奇函数，故其图象关于原点中心对称．排除B，C．
又当0＜x＜1＜
| π |
| 2 |
故选A．
练习册系列答案
相关题目
，函数
.
时，函数
的图象与函数
的图象有公共点，求实数
的最大值；
时，试判断函数
的上方？若能，求出
的取值范围；若不能，请说明理由．
．
的方程f(x)=a在区间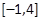
上有两个根,求a的取值范围．