题目内容
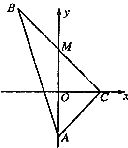
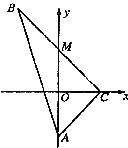 如图所示,△ABC为直角三角形,∠C=90°,若
如图所示,△ABC为直角三角形,∠C=90°,若![]() =(0,-4),M在
=(0,-4),M在![]() 轴上,且AM=
轴上,且AM=![]() ,点C在
,点C在![]() 轴上移动.
轴上移动.
(Ⅰ)求点B的轨迹E的方程;
(Ⅱ)过点F(0,![]() )的直线
)的直线![]() 与曲线E交于P、Q两点,设N(0,
与曲线E交于P、Q两点,设N(0,![]() )(
)(![]() <0),
<0),![]() 与
与![]() 的夹角为
的夹角为![]() ,若
,若![]() ≤
≤![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)设以点N为圆心,以![]() 半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求
半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求![]() 的值.
的值.
解:(Ⅰ)∵![]() ∴M是BC的中点
∴M是BC的中点
设B(![]() )则M(O,
)则M(O,![]() ),C(-
),C(-![]() ,0)
,0)
![]()
∵∠C=90° ∴OB⊥CA ![]()
(![]() )?(
)?(![]() )=0 ∴
)=0 ∴ ![]()
(Ⅱ)设直线![]() 方程为
方程为![]()
![]() ,
,
由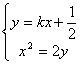 知
知![]()
∴ ![]()
由![]() 知(
知(![]() )?(
)?(![]() )≥0
)≥0
![]()
又![]()
∴![]()
∴ 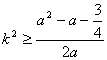 恒成立
恒成立
∴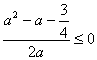 又
又![]()
∴![]()
(Ⅲ)由题意知,NH是曲线C的切线,设![]()
则![]() ,
,![]()
∴![]() .
.
又因![]() ,
, ![]()
消去![]() 得
得![]()
解得![]() 或
或![]()
∵![]()
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
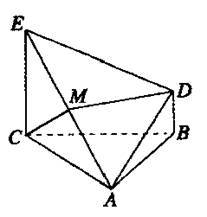
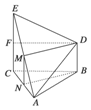
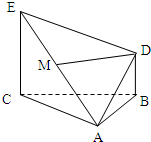 如图所示,△ABC为正三角形,EC⊥底面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,
如图所示,△ABC为正三角形,EC⊥底面ABC,BD∥CE,且CE=CA=2BD,M是EA的中点,