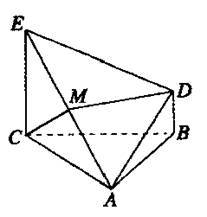
题目内容
如图所示，△ABC为正三角形,EC⊥平面ABC,BD∥CE,且CE=CA=2BD,M是EA中点.
求证:(1)DE=DA;
(2)平面MBD⊥平面ECA;
(3)平面DEA⊥平面ECA.
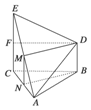
证明：(1)取EC的中点F,连结DF.?
∵EC⊥平面ABC,∴EC⊥BC.?
∵CE=2BD,∴BD=CF.?
又∵BD∥CE,∴BDCF.?
∴BDFC是平行四边形.∴BC
DF.∴DF⊥EC.?
在Rt△EFD和Rt△DBA中,?
∵EF=12EC=BD,FD=BC=AB(∵△ABC是正三角形,∴BC=CA=AB),
∴Rt△FED≌Rt△DBA.∴DE=DA.?
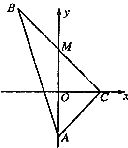
另解：取AC中点N,连结BN、MN.?
∵△ABC是正三角形,∴BN⊥AC于N.?
又∵EC⊥面ABC,EC
面CAE，?
∴面ACE⊥面ABC，交线为AC.?
∴BN⊥平面ACE.?
又∵M、N分别是AE、AC中点,?
在△ACE中,ME 
CE,?
又BD∥CE且2BD=CE，?
∴BD 
CE 
MN.?
∴四边形BDMN是平行四边形.∴MD
BN.?
∴DM⊥平面ACE.?
又AE
平面ACE,∴DM⊥AE于M.?
又∵M是AE中点,且MD⊥AE,∴DA=DE.?
(2)取CA的中点N,连结MN、BN,则MN
EC.?
又∵BD∥EC,∴MN
DB.?
∴N点在平面BDM内.?
∵EC⊥平面ABC,BN
平面MBD.?
∴面MBN⊥平面ECA,
即平面MBD⊥平面ECA.?
(3)DM∥BN,BN⊥平面ECA,∴DM⊥平面ECA.?
又DM
平面DEA,∴平面DEA⊥平面ECA.
练习册系列答案
阅读快车系列答案
相关题目
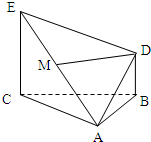如图所示，△ABC为正三角形，EC⊥底面ABC，BD∥CE，且CE=CA=2BD，M是EA的中点，
=(0，-4)，M在
轴上，且AM=
，点C在
轴上移动．
)的直线
与曲线E交于P、Q两点，设N(0，
)(
与
的夹角为
，若
等恒成立，求
半径的圆与曲线E在第一象限的交点为H，若圆在点H处的切线与曲线E在点H处的切线互相垂直，求