Question

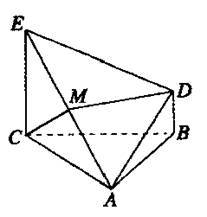
（08年聊城市三模）（12分）   如图所示，△ABC为正三角形，EC⊥平面ABC，BD∥CE，且CE=CA=2BD，M是EA的中点.

   （I）证明：DM∥平面ABC；

   （II）证明：CM⊥DE；

   （III）求平面ADE与平面ABC所成的二面角的大小（只考虑锐角情况）.

 

Answer 1

解析:证明：（I）取AC的中点N，又M为AE中点，则

∵BD//CE，且BD=，

∴四边形BDMN为平行四边形，则DM//BN.

平面ABC，∴DM//平面ABC.…………4分

   （II）∵△ABC为正三角形且N为AC中点，

∴BN⊥AC.∵EC⊥平面ABC，∴EC⊥BN.

∴BN⊥平面ACE.∴CM⊥BN.

∵DM∥BN，∴CM⊥DM.

∵CE=CA，且M为AE中点，

∴CM⊥AE.又AE∩MD=M.∴CM⊥平面ADE.

又∵DE平面ADE，∴CM⊥DE.…………8分

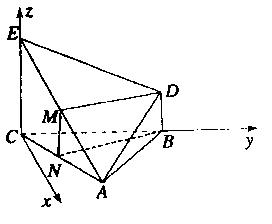
   （III）以C为原点，过C且垂直于CB的直线为x轴，CB所在直线为y轴，建立空间直角坐标系（如图），设CE=1，则

   

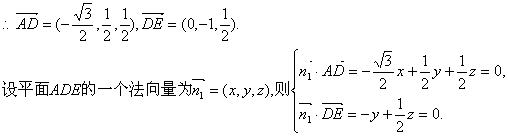
    令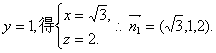                     …………10分

   

    ∴平面ADE与平面ABC所成的锐二面角的大小为45°.       …………12分