题目内容
已知sinα,cosα是方程25x2-5(2t+1)x+t2+t=0的两根,且α为锐角.(1)求t的值;
(2)求以
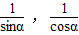 为两根的一元二次方程.
为两根的一元二次方程.
【答案】分析:(1)根据已知中sinα,cosα是方程25x2-5(2t+1)x+t2+t=0的两根,由韦达定理可得sinα+cosα=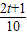 ,sinα•cosα=
,sinα•cosα=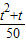 ,根据sin2α+cos2α=(sinα+cosα)2-2•sinα•cosα=1,我们构造关于t的方程,求出t的值;
,根据sin2α+cos2α=(sinα+cosα)2-2•sinα•cosα=1,我们构造关于t的方程,求出t的值;
(2)设以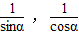 为两根的一元二次方程为y2+by+c=0,由韦达定理分别求出b,c的值即可得到满足条件的方程.
为两根的一元二次方程为y2+by+c=0,由韦达定理分别求出b,c的值即可得到满足条件的方程.
解答:解:(1)∵sinα,cosα是方程25x2-5(2t+1)x+t2+t=0的两根,
∴sinα+cosα=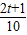 ,sinα•cosα=
,sinα•cosα=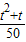
∴sin2α+cos2α=(sinα+cosα)2-2•sinα•cosα=(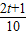 )2-2•
)2-2•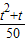 =1
=1
解得t=3,t=-4
又∵α为锐角
∴t>0,故t=-4(舍去)
∴t=3,
(2)由(1)可得sinα+cosα=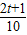 =
=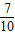 ,sinα•cosα=
,sinα•cosα=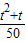 =
=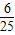
设以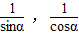 为两根的一元二次方程为y2+by+c=0
为两根的一元二次方程为y2+by+c=0
则-b=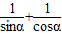 =
=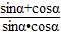 =
=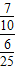 =
=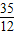
∴b=-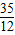
C=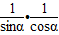 =
=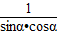 =
=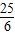
∴以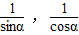 为两根的一元二次方程
为两根的一元二次方程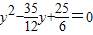
点评:本题考查的知识点是三角函数恒等变换,韦达定理(一元二次方程根与系数的关系),熟练掌握韦定定理,是解答本题的关键,其中(1)中易忽略α为锐角,而错解为t=3,或t=-4.
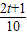 ,sinα•cosα=
,sinα•cosα=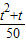 ,根据sin2α+cos2α=(sinα+cosα)2-2•sinα•cosα=1,我们构造关于t的方程,求出t的值;
,根据sin2α+cos2α=(sinα+cosα)2-2•sinα•cosα=1,我们构造关于t的方程,求出t的值;(2)设以
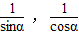 为两根的一元二次方程为y2+by+c=0,由韦达定理分别求出b,c的值即可得到满足条件的方程.
为两根的一元二次方程为y2+by+c=0,由韦达定理分别求出b,c的值即可得到满足条件的方程.解答:解:(1)∵sinα,cosα是方程25x2-5(2t+1)x+t2+t=0的两根,
∴sinα+cosα=
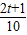 ,sinα•cosα=
,sinα•cosα=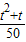
∴sin2α+cos2α=(sinα+cosα)2-2•sinα•cosα=(
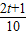 )2-2•
)2-2•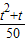 =1
=1解得t=3,t=-4
又∵α为锐角
∴t>0,故t=-4(舍去)
∴t=3,
(2)由(1)可得sinα+cosα=
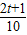 =
=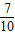 ,sinα•cosα=
,sinα•cosα=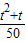 =
=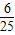
设以
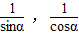 为两根的一元二次方程为y2+by+c=0
为两根的一元二次方程为y2+by+c=0则-b=
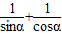 =
=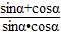 =
=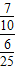 =
=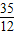
∴b=-
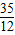
C=
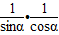 =
=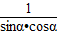 =
=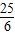
∴以
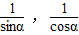 为两根的一元二次方程
为两根的一元二次方程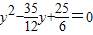
点评:本题考查的知识点是三角函数恒等变换,韦达定理(一元二次方程根与系数的关系),熟练掌握韦定定理,是解答本题的关键,其中(1)中易忽略α为锐角,而错解为t=3,或t=-4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目