题目内容
若在曲线 上两个不同点处的切线重合,则称这条切线为曲线
上两个不同点处的切线重合,则称这条切线为曲线 或
或 的“自公切线”。
的“自公切线”。
下列方程:
① ;
;
② ;
;
③ ;
;
④
对应的曲线中存在“自公切线”的有( )
| A.①③ | B.①④ | C.②③ | D.②④ |
C
解析试题分析:①x2-y2=1 是一个等轴双曲线,没有自公切线;
② ,在 x=
,在 x= 和 x=-
和 x=- 处的切线都是y=-
处的切线都是y=- ,故②有自公切线.
,故②有自公切线.
③ =5sin(x+φ),cosφ=
=5sin(x+φ),cosφ= ,sinφ=
,sinφ= ,此函数是周期函数,过图象的最高点的切线都重合或过图象的最低点的切线都重合,故此函数有自公切线.
,此函数是周期函数,过图象的最高点的切线都重合或过图象的最低点的切线都重合,故此函数有自公切线.
④ ,即 x2+2|x|+y2-3=0,结合图象可得,此曲线没有自公切线.
,即 x2+2|x|+y2-3=0,结合图象可得,此曲线没有自公切线.
故答案为②③.选C。
考点:圆锥曲线的几何性质,分段函数的概念,三角函数辅助角公式,三角函数的图象和性质。
点评:中档题,本题综合性较强,考查知识点覆盖面广。正确理解新定义“自公切线”,利用数形结合思想,正确画出函数的图象,是解题的关键。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
已知函数 对于任意的
对于任意的 ,导函数
,导函数 都存在,且满足
都存在,且满足 ≤0,则必有( )
≤0,则必有( )
A. > > | B. ≤ ≤ |
C. < < | D. ≥ ≥ |
下列函数中,为偶函数且有最小值的是 ( )
| A.f(x) =x2 +x | B.f(x) = |lnx| |
| C.f(x) =xsinx | D.f(x) =ex+e-x |
已知f(x)是实数集上的偶函数,且在区间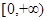 上是增函数,则
上是增函数,则 的大小关系是( )
的大小关系是( )
A. | B. |
C. | D. |
已知定义在 上的函数
上的函数 满足
满足 ,当
,当 时,
时, 单调递增,若
单调递增,若 且
且 ,则
,则 的值( )
的值( )
| A.可能为0 | B.恒大于0 | C.恒小于0 | D.可正可负 |
函数f(x)=㏑x的图像与函数g(x)=x2-4x+4的图像的交点个数为
| A.0 | B.1 | C.2 | D.3 |
已知函数 的定义域为
的定义域为 ,
, 的定义域为
的定义域为 ,则
,则 ( )
( )
A.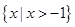 | B. | C. | D. |
若 上是减函数,则
上是减函数,则 的取值范围是( )
的取值范围是( )
A. | B. | C.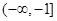 | D. |
 的大致图象是( )
的大致图象是( )