题目内容
【题目】已知某校中小学生人数和近视情况分别如图所示.为了解该校中小学生的近视形成原因，用分层抽样的方式从中抽取一个容量为50的样本进行调查.
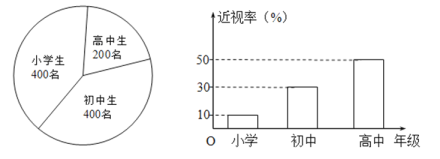
（1）求样本中高中生、初中生及小学生的人数；
（2）从该校初中生和高中生中各随机抽取1名学生，用频率估计概率，求恰有1名学生近视的概率；
（3）假设高中生样本中恰有5名近视学生，从高中生样本中随机抽取2名学生，用
表示2名学生中近视的人数，求随机变量的分布列和数学期望.
【答案】（1）10，20，20，（2）0.5 （3）分布列见解析，
【解析】
（1）利用分层抽样计算高中生、初中生及小学生的人数即可.
（2）首先设事件
为“从该校初中生抽取1名学生是近视”，事件
为“该校高中生抽取1名学生是近视”，分别计算出
，
，再利用概率公式
计算即可.
（3）先求出
的所有取值及对应的概率，列出分布列，计算数学期望即可.
（1）采用分层抽样，样本容量与总体容量的比为：
，
所以样本中高中生、初中生及小学生的人数分别为：10，20，20.
（2）设事件为“从该校初中生抽取1名学生是近视”，
事件为“该校高中生抽取1名学生是近视”.
由题意知：
，
，
故所求概率为.
故所求概率为：
.
（3）随机变量的所有可能取值为：0，1，2.
，
，
.
所以随机变量的分布列为：
| 0 | 1 | 2 |
|
|
|
|
所以
.
练习册系列答案
相关题目
